Chapter 17: Sorbarendezés

Bináris keresés csak akkor működik listákon, ha azok sorrendben vannak. Szóval, hogyan lehetséges a listát rendezni? Hogyan rendezhet egy program elemi listákat úgy, hogy a felhasználó csak kattint egyet.

Számos algoritmus létezik erre. A két legkönnyebb algoritmus a kiválasztásos rendezés és a beszúrásos rendezés. Másféle rendezéses algoritmusok is léteznek, mint amilyen a buborékos-, gyorsrendezés, fésűs rendezés.

A legjobb útja annak, hogy megértsük, ahogyan ez működik, ha látjuk őket működés közben. Ehhez látogass el erre a weboldalra:
http://www.sorting-algorithms.com

Minden rendezésnek van egy előnye és egy hátránya. Némely rendezés gyors, ha a lista már amúgy is sorrendben volt. Mások akkor is gyorsak, ha a lista az elején össze volt keverve. Más listarendezések pedig gyorsak, de sok memóriát fogyasztanak. A működésük megértése azért fontos, hogy a helyes eljárást választhasd majd a programodhoz.

17.1 Értékek megcserélése

Mielőtt még a rendezést megtanulnánk, fontos megismerni azt, hogyan cseréljünk meg értéket két változó közt. Ez egy gyakori művelet sok algoritmusban. Mondjuk van egy programunk, egy alább kinéző listával:

list = [15,57,14,33,72,79,26,56,42,40]

A fejlesztő azt szeretné, hogy a 0 és a 2 helyzetét megcserélje, ami a 15-s és 14-s számot tartalmazza. Lásd alább: 17.1.

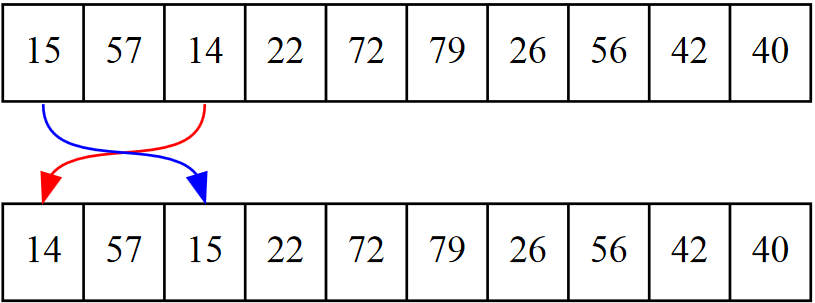
Első ránézésre az ember hajlamos arra, hogy egy ilyen kódra gondoljon:

list[0] = list[2]
list[2] = list[0]

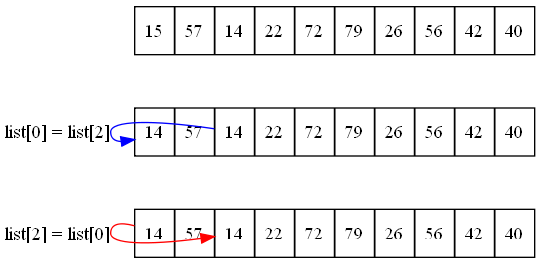
Lásd az ábrát17.2, hogy megértsd mi történik. Ez természetesen nem fog működni. Az első állítás a list[0] = list[2] azt fogja elérni, hogy a 15-s értéket a 0-dik helyen felül fogja írni a 14-s érték a 2-dik helyről, és az első értékünk el is vesződik. A következő sor a list[2] = list[0] csak annyit tesz, hogy a 14-s értéket a 2-s cellából visszamásolja, ami már amúgy is 14.

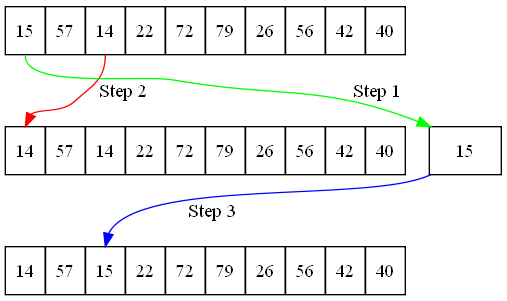
A probléma megoldása, hogy a tömb értékeit úgy cseréljük meg, hogy három lépést veszünk igénybe. Ehhez szükséges létrehozni egy ideiglenes változót, ami majd tárolja az értéket a csere során. Lásd az ábrát:17.3. A kód, ami meg fogja oldani a cserét így néz ki:

temp = list[0]
list[0] = list[2]
list[2] = temp

Az első sor lemásolja a 0-s helyen lévő értéket a temp változóba. Ez lehetővé teszi a kód számára, hogy a 0-s cellába írjon, anélkül, hogy adatvesztés lépne fel. Az utolsó sorban a 0-s pozíció értéke a temp változóból kerül át a 2-s cellába.

17.2 Kiválasztásos rendezés

A kiválasztásos rendezés a lista elején kezd. Azután a kód végignézi a maradék listát, hogy megtalálja a legkisebb számot. a legkisebb szám azután helyet cserél. A kód a következő számra mozog. Grafikusan a kiválasztás így néz ki: 17.4.

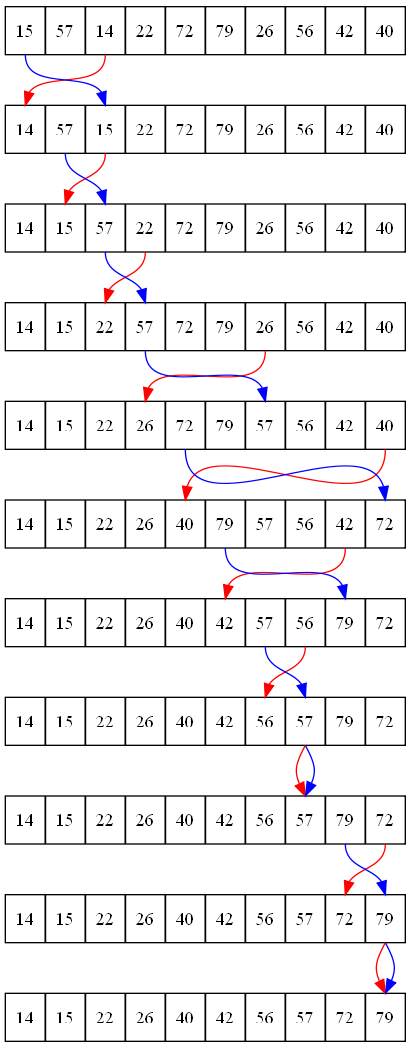
A kód a kiválasztásos rendezéshez két egymásba ágyazott ciklust igényel. A külső ciklus követi nyomon a pozíciót, amit a kód szeretne megcserélni a legkisebb értékkel. A belső ciklus elindul az aktuális helyről és végignézi jobbra az összes értéket a legkisebbet keresve. Amikor megtalálja, akkor megcseréli a két helyet.

# A kiválasztásos rendezés
def selection_sort(list):

    # Végigfut a teljes tömbön a ciklus
    for curPos in range( len(list) ):
	    # Találjuk meg a helyet, ahol a legkisebb szám van
	    # ezdjük az aktuális hellyel
        minPos = curPos

        # Balról jobbra haladunk a lista végéig
        for scanPos in range(curPos+1, len(list) ):

            # Kisebb?
            if list[scanPos] < list[minPos]:

                # Igen, jegyezzük meg, hogy kisebb
                minPos = scanPos

        # Cseréljük meg a két értéket
        temp = list[minPos]
        list[minPos] = list[curPos]
        list[curPos] = temp

A külső ciklus mindig $n$-szer fog lefutni. A belső ciklus $n/2$ alkalommal fut le. Ez annak ellenére történik, mégha a lista rendezett lenne is. A ciklus hatékonyságát lehet növelni, ha ellenőrízzük a minPos és curPos egyenlőségéet a 16-s sorban. Ha ez a két változó egyenlő, akkor nincs szükségünk a három sornyi cserére.

Azért, hogy a fenti rendezéses kódot teszteljük, a következő kódot használhatjuk. Az első függvény ki fogja íratni a listát. A következő kód egy véletlenszerű számsort generál, majd rendezi, és kiírja. A harmadik sorban a print parancs jobbra rendezi a számokat, hogy könnyebben olvasható legyen. A print parancs formatálásról majd a 20-dik fejezetben adunk bővebb felvilágosítást.

# Mielőtt ez a kód lefutna, illeszd be a kiválasztásos rendezés kódját és importáld a random függvényt

def print_list(list):
    for item in list:
        print("{:3}".format(item), end="")
    print()

# véletlenszerű számsor létrehozása
list = []
for i in range(10):
    list.append(random.randrange(100))

# A puding próbája
print_list(list)
selection_sort(list)
print_list(list)

Nézzünk egy animációt a kiválasztásos rendezésről:
http://www.sorting-algorithms.com/selection-sort

Valóban egyedi megjelenítése a kiválasztásos rendezésnek található a youtube-on, csak keress rá a "selection sort dance" kifejezésre:
http://youtu.be/Ns4TPTC8whw

Nyomon követheted a kódot azzal, ha használod a http://pythontutor.com-t.

17.3 Beillesztéses rendezés

A beillesztéses rendezés hasonló a kiválasztásos sorbarendezéshez,abban, ahogyan a külső ciklus működik. A beillesztés elkezdődik a tömb bal oldalán és a jobb oldalig fut. A különbség az, hogy a beillesztés során nem választjuk ki a legkisebb elemet, és nem is tesszük sehová; a beillesztéses rendezés kiválasztja a következő elemet jobbról, amit már rendezett. Azután a nagyobb elemeket mindig feljebb csúsztatja amíg, minden a helyére nem kerül. Grafikusan így néz ez ki: 17.5.

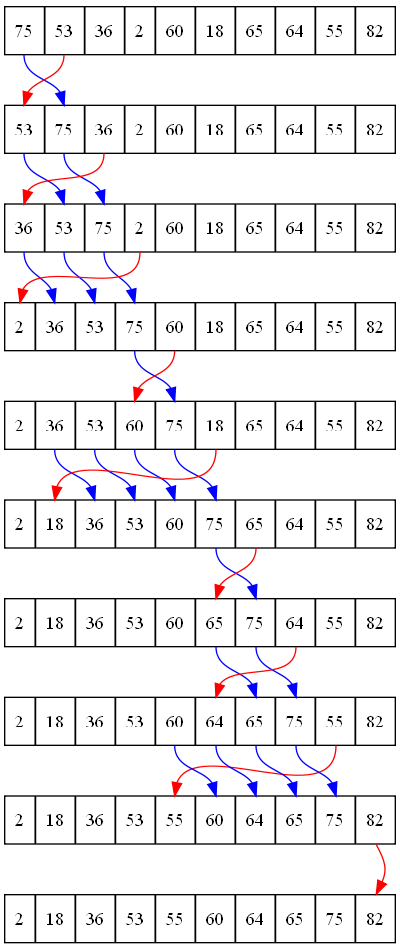
A beillesztéses rendezés két részre szakítja a listát, a rendezett felére és a rendezetlen felére. Minden körben a külső ciklus végrehajtása során az algoritmus fogja a következő rendezetlen elemet és beilleszti a listába.

A lenti kódban a keyPos jelzi a határokat a rendezett és a rendezetlen lista részek közt. Az algoritmus végignézi a baloldalát a keyPos változónak, amihez a scanPos változót használja. Jegyezd meg, hogy a beillesztés rövid, a scanPos lefelé tart balra, és nem felfelé jobbra. Minden cella helyzete, ami nagyobb, mint a keyValue fel fog mozogni egyet, jobbra.

Amikor a ciklus megleli a helyét annak, ami kisebb, mint a keyValue, megáll és beilleszti a keyValue-tól balra.

A külső ciklus a beillesztéses rendezésnek $n$-szer fog lefutni. A belső része átlagosan $n/2$ alkalomszor, ha a lista véletlenszerűen van összekeverve. Ha a ciklus közel van egy rendezett ciklushoz, akkor a belső ciklus nem fog lefutni annyiszor, hanem közel $n$-szer csak.

def insertion_sort(list):

    # Induljon el a második elemtől (pos 1).
    # használjuk ezt az elemet és illesszük be a listába
    for keyPos in range(1, len(list)):

        # Adjunk értéket az elemnek, amit beillesztünk
        keyValue = list[keyPos]

        # keressünk jobbról balra (lista kezdete felé)
        scanPos = keyPos - 1

        # Ismételjünk minden elemt, mozgassuk
        # amíg elérjük a pozíciót
        while (scanPos >= 0) and (list[scanPos] > keyValue):
            list[scanPos + 1] = list[scanPos]
            scanPos = scanPos - 1

        # Minden el lett vive az útból, illesszük be
        # a kulcsot a megfelelő helyre
        list[scanPos + 	1] = keyValue

Nézzünk meg egy animációt a beillesztéses rendezésről:
http://www.sorting-algorithms.com/selection-sort

Másik táncos értelmezés, ha rákeresel a Youtube-n az “insertion sort dance” kifejezésre, vagy az alábbi linken:
http://youtu.be/ROalU379l3U

Nyomon követheted a kódot itt is: http://pythontutor.com.

17.3.1 Kvízkérdések

Click here for a multiple-choice quiz.

17.3.2 Feladatlapok

Click here for the chapter worksheet.

You are not logged in. Log in here and track your progress.