Arcade-pelien ohjelmointi Pythonilla ja Pygamella
Chapter 17: Lajittelu
Binaarihaku toimii vain, jos lista on lajiteltu. Miten listan saisi lajiteltua järjestykseen? Miten ohjelma lajittelee taulukon alkiot, kun hiirellä klikataan otsikkoriviä?
Lajitteluun on olemassa useita algoritmeja. Kaksi yksinkertaisinta lasjittelualgoritmia ovat valintalajittelu ja lisäyslajittelu. Muitakin lajittelualgoritmeja on; esim. kuplalajittelu, kekolajittelu, vaihtolajittelu, limityslajittelu jne.
Parhaiten lajittelun toiminnan oppii tutkimalla, miten se toimii käytännössä.
Tämän voit tehdä vaikkapa tällä loistavalla nettisivulla:
http://www.sorting-algorithms.com
Kullakin lajittelualgoritmilla on tiettyjä etuja ja haittoja. Joku algoritmi lajittelee listan nopeasti, jos lista on jo melkein lajiteltu. Toinen taas lajittelee nopeasti, jos lista on järjestetty satunnaisesti. Jokin algoritmi lajittelee nopeasti, mutta vaatii lajitteluun paljon (muisti)tilaa. Lajitteluiden ymmärtäminen on tärkeää valittaessa omaan ohjelmaan sopivaa lajittelualgoritmia.
17.1 Arvojen vaihto eli swappi
Ennen lajittelun opiskelua selvitämme sen, miten saamme vaihdettua kahden muuttujan arvot keskenään. Tämä 'swappi' on varsin keskeinen toimenpide monissa lajittelualgoritmeissa. Oletetaan, että meillä on alla kuvattu lista:
list = [15,57,14,33,72,79,26,56,42,40]
Koodaaja haluaa vaihtaa indeksien 0 ja 2 sisältöjen paikkaa keskenään, siis lukujen 15 ja
14 vaihto. Katso kuva 17.1.
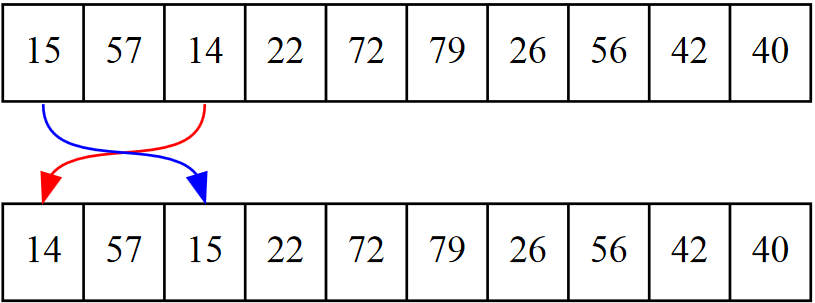
Ensimmäinen mieleen tuleva ratkaisu voisi näyttää tältä:
list[0] = list[2] list[2] = list[0]
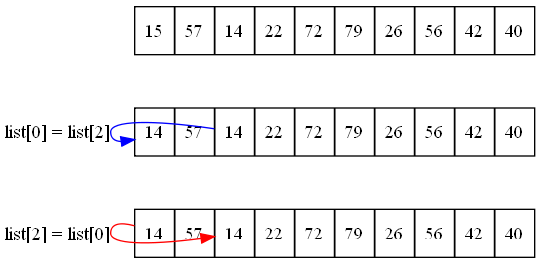
Katso kuvaa 17.2 ja huomaat, mitä tässä tapahtuu. Tämä ei siis toimi. Ensimmäinen asetuslause list[0] = list[2] saa aikaan sen, että indeksissä 0 oleva luku 15 korvataan luvulla 14. Luku 15 menetetään lopullisesti. Seuraava rivi list[2] = list[0] ainoastaan kopioi luvun paikasta 0 paikkaan 2 ja sehän on nyt luku 14.
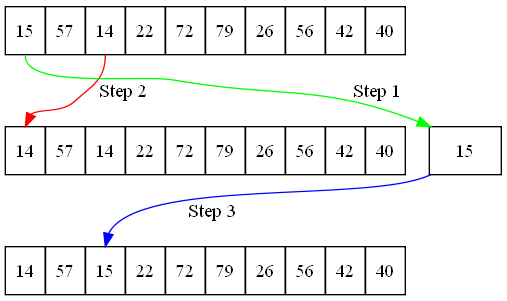
Tämä ongelma saadaan ottamalla käyttöön väliaikainen muuttuja temp, johon toinen vaihdettava luku tallennetaan väliaikaisesti. Ensimmäisen vaihdon jälkeen väliaikainen muuttuja temp kopioidaan toisen muuttujan arvoksi. Katso kuva 17.3. Swappauksen suorittava koodi näyttää seuraavalta:
temp = list[0] list[0] = list[2] list[2] = temp
Ensimmäisellä rivillä kopioidaan paikan 0 arvo temp muuttujan arvoksi.
Tämän jälkeen paikan 0 luku voidaan korvata paikan 2 arvolla. Lopuksi paikan 0 arvo saadaan
palautettua temp muuttujasta ja sijoitettua paikkaan 2.
17.2 Valintalajittelu
Valintalajittelu lajittelee listan suuruusjärjestykseen siten, että otetaan ensimmäisen alkion arvo ja
verrataan sitä vuorollaan kuhunkin listassa n-1 jäljellä olevaan alkioon. Jos löytyy pienempi alkio, niin
vaihdetaan se paikkaan 0. Ensimmäisen vartailu/vaihtokierroksen jälkeen siirrytään alkioon 1 paikassa ja taas verrataan jäljellä oleviin alkiohin
ja tehdään vaihto tarvittaessa. Graafisesti valintalajittelun voio esittää kuten kuvassa 17.4.
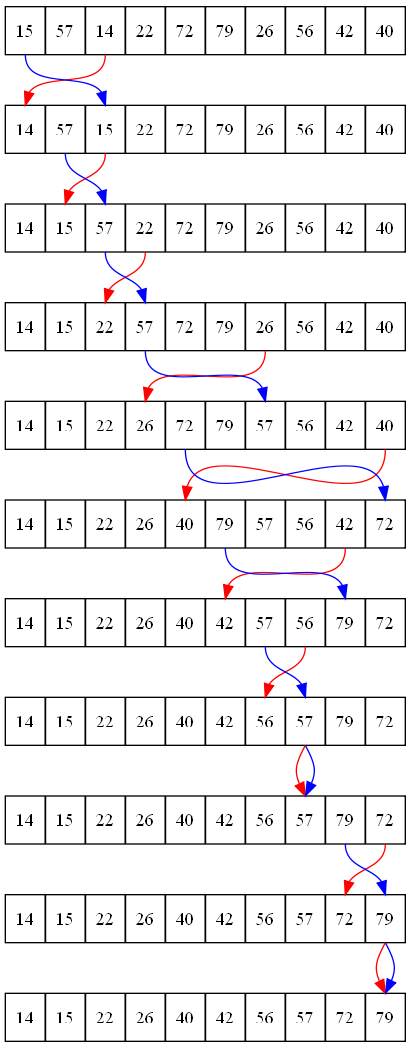
Valintalajittelun implementointiin tarvitaan kaksi sisäkkäistä silmukkaa. Ulompi silmukka askeltaa listan lukua aloittaen paikasta 0, johon etsitään sisemmässä silmukassa listan pienintä alkiota. JOs pienempi alkio löytyy, se swapataan paikkaan 0 (1,2,jne.).
def selection_sort(list):
""" Sort a list using the selection sort """
# Loop through the entire array
for cur_pos in range(len(list)):
# Find the position that has the smallest number
# Start with the current position
min_pos = cur_pos
# Scan left to right (end of the list)
for scan_pos in range(cur_pos + 1, len(list)):
# Is this position smallest?
if list[scan_pos] < list[min_pos]:
# It is, mark this position as the smallest
min_pos = scan_pos
# Swap the two values
temp = list[min_pos]
list[min_pos] = list[cur_pos]
list[cur_pos] = temp
Ulompi silmukka suoritetaan aina $n$ kertaa. Sisempi silmukka suoritetaan $n/2$ kertaa. Nämä suoritusmäärät tehdään aina huolimatta siitä, onko lista valmiiksi järjestyksessä vai ei. Silmukan tehokkuutta saadaan parannettua tarkistamalla, onko minPos ja curPos yhtäsuuret ennen riviä 16. Jos ne ovat samat, niin swappaus voidaan jättää suorittamatta.
Valintalajittelun koodi voidaan testata alla olevalla esimerkkiohjelmalla. Ensimmäisenä oleva funktio tulostaa listan. Seuraavaksi koodissa luodaan satunnaislukujen lista, tulostetaan se, lajitellaan ja tulostetaan uudelleen. Rivillä 3 print lauseessa muotoillaan luvut tulostumaan sarakkeisiin oikeaan reunaan lukemisen helpottamiseksi. Tulostuksen muotoilua käsitellään kappaleessa 20.
# Liitä ennen tätä koodia valintalajittelun koodi ja myös import random
def print_list(list):
for item in list:
print("{:3}".format(item), end="")
print()
# Create a list of random numbers
list = []
for i in range(10):
list.append(random.randrange(100))
# Try out the sort
print_list(list)
selection_sort(list)
print_list(list)
Katso valintalajittelusta animaatio:
http://www.sorting-algorithms.com/selection-sort
Todella yksityiskohtainen valintalajittelun visualisointi löytyy YouTubesta hakutermillä
“selection sort dance” tai tästä linkistä:
http://youtu.be/Ns4TPTC8whw
Voit kahlata koodin läpi myös tästä: http://pythontutor.com.
17.3 Lisäyslajittelu
Lisäyslajittelu muistuttaa valintalajittelyua varsinkin ulomman silmukan
toiminnan osalta. Algoritmi toimii pitämällä taulukon alkuosan koko ajan järjestyksessä
lisäämällä yksitellen jokaisen alkion käsittelemättömästä loppuosasta oikealle paikalleen alkuosaan.
Erona valintalajitteluun on siis, että lisäyslajittelussa ei haeta pieninta alkiota,
vaan otetaan listan seuraava alkio ja lisätään se listan alkuun oikeaan kohtaan.
Graafisesti esitettynä algoritmi voisi olla oheisen kuvan kaltainen.
Figure 17.5.
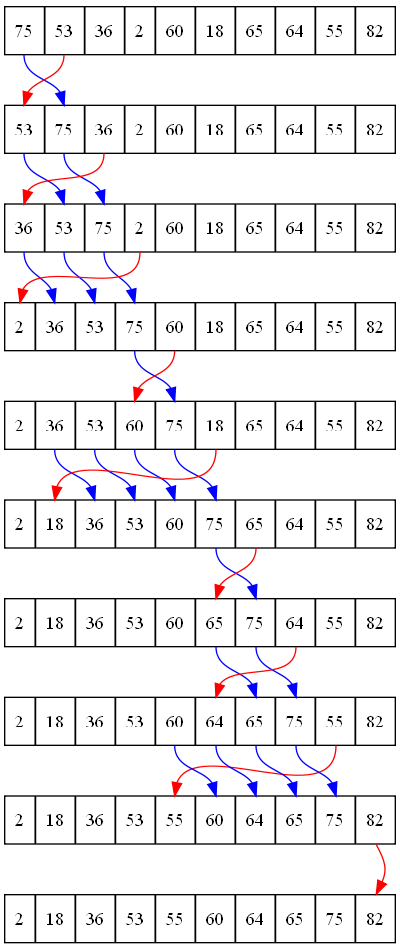
Lisäyslajittelu jakaa listan kahteen osaan. Toinen on “lajiteltu” osa ja toinen “lajittelematon” osa. Jokaisella ulomman silmukan kierroksella algoritmi nappaa seuraavan lajittelemattoman alkion ja sijoittaa sen listaan oikealle paikalle.
Alla esimerkkikoodissa keyPos merkkaa rajakohdan lajitellun ja lajittelemattoman listan osan välille. Algoritmi 'skannaa' vasemman puoleisen osan oikealta vasemmalle aloittaen keyPos kohdasta ja askeltaen alaspäin muuttujalla scanPos. Huomaathan siis, että lisäyslajittelun lisäyskohta haetaan scanPos muuttujalla. Jokainen arvo (indeksi) joka on suurempi kuinkeyValue siirretään ylöspäin siis oikealle yhden indeksin verran.
Kun silmukassa löytyy keyValue pienempi arvo, pysähtyy silmukka ja asetetaan keyValue tämän paikan vasemmalle puolelle.
Ulompi silmukka suoritetaan lisäyslajittelussa $n$ kertaa. Sisempi silmukka suoritetaan keskimäärin $n/2$ kertaa, jos silmukka suoritetaan sattumanvaraisesti. Jos lista on lähestulkoon lajiteltu valmiiksi, niin sisempää silmukkaa ei juurikaan suoriteta, jolloin lajitteluaika on lähempänä $n$.
def insertion_sort(list):
""" Sort a list using the insertion sort """
# Start at the second element (pos 1).
# Use this element to insert into the
# list.
for key_pos in range(1, len(list)):
# Get the value of the element to insert
key_value = list[key_pos]
# Scan from right to the left (start of list)
scan_pos = key_pos - 1
# Loop each element, moving them up until
# we reach the position the
while (scan_pos >= 0) and (list[scan_pos] > key_value):
list[scan_pos + 1] = list[scan_pos]
scan_pos = scan_pos - 1
# Everything's been moved out of the way, insert
# the key into the correct location
list[scan_pos + 1] = key_value
Katso tästä lisäyslajittelun visualisointi:
http://www.sorting-algorithms.com/insertion-sort
Toinen tanssi löytyy hakemalla YouTubesta hakutermillä
“insertion sort dance” tai käyttäen tätä linkkiä:
http://youtu.be/ROalU379l3U
Lisäyslajittelun koodin voit käydä läpi myös tästä http://pythontutor.com.
17.3.1 Multiple Choice Quiz
Klikkaa tästä monivalintatehtävään.
17.3.2 Short Answer Worksheet
Klikkaa tästä kappaleen kertaustehtäviin.
English version by Paul Vincent Craven
Spanish version by Antonio Rodríguez Verdugo
Russian version by Vladimir Slav
Turkish version by Güray Yildirim
Portuguese version by Armando Marques Sobrinho and Tati Carvalho
Dutch version by Frank Waegeman
Hungarian version by Nagy Attila
Finnish version by Jouko Järvenpää
French version by Franco Rossi
Korean version by Kim Zeung-Il
Chinese version by Kai Lin