Chapter 17: Poniendo Orden

Las búsquedas binarias solo funcionan en listas que se encuentren ordenadas. Entonces, cómo hacemos que nuestros programas reciban una lista ordenada? ¿Cómo es que un programa ordena una lista de objetos al hacer click sobre el encabezado de una columna?

Existen distintos algoritmos para hacerlo. Los dos algoritmos más simples para conseguirlo son los llamados de ordenamiento por selección y de ordenamiento por inserción. Existen algunos otros como los shell, por mezcla, montículo y quicksorts.

La mejor forma de tener una idea de cómo funcionan es verlos trabajar. Para ver los algoritmos de ordenamiento más comunes en acción, visita este excelente website:
http://www.sorting-algorithms.com

Cada clase de ordenamiento tiene sus pros y sus contras. Algunos ordenan rápidamente una lista si ésta se encuentra casi ordenada al empezar. Otros lo hacen con listas donde el orden es totalmente aleatorio. Otros lo hacen muy rápido, pero a un alto coste de memoria. Comprender cómo funciona un ordenamiento es clave para seleccionar el algoritmo adecuado para un programa.

17.1 Intercambiando Valores

Antes de aprender cómo ordenar, debemos aprender cómo intercambiar valores entre dos variables. Esta es una operación muy común en muchos de estos algoritmos. Imaginemos que tenemos una lista con el aspecto siguiente:

lista = [15, 57, 14, 33, 72, 79, 26, 56, 42, 40]

Digamos que el desarrollador quiere intercambiar las posiciones 0 y 2, que contienen los números 15 y 14 respectivamente. Observa la Figura 17.1.

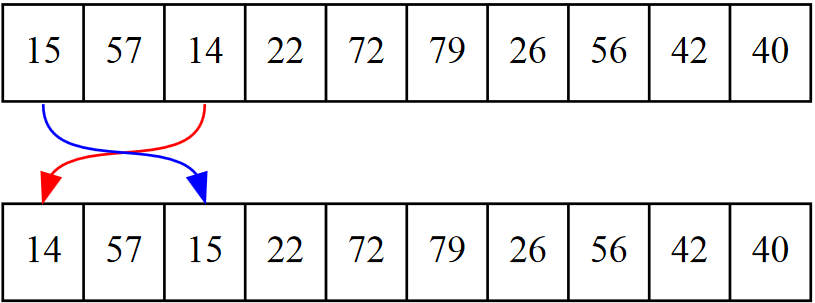
Un primer intento para desarrollar el código podría ser éste:

lista[0] = lista[2]
lista[2] = lista[0]

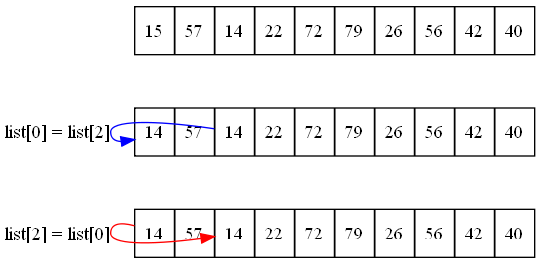
Observa la Figura 17.2 para que tengas una idea de lo que sucedería. Claramente no funciona. La primera asignación lista[0] = lista[2] provoca que el valor 15 de la posición 0 sea sobrescrito por el valor 14 de la posición 2, e irremediablemente perdido. La línea siguiente, lista[2] = lista[0], tan solo vuelve a copiar el valor 14 a la celda 2, que ya posee ese mismo valor.

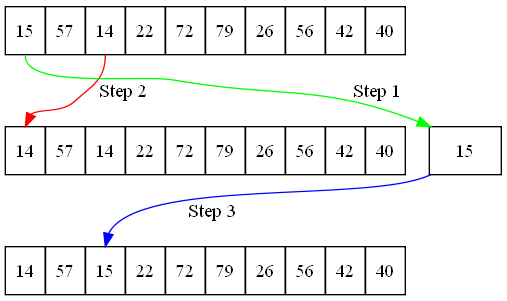
Para arreglar este problema, el intercambio de valores en un array debería hacerse en tres pasos. Para ello es necesario crear una variable temporal que guarde un valor durante la operación de intercambio. Observa la Figura 17.3. El código para hacerlo sería el siguiente:

temp = lista[0]
lista[0] = lista[2]
lista[2] = temp

La primera línea copia el valor de la posición 0 en la variable temp. Esto permite que en la línea 2, el código sobrescriba la posición 0 con el valor de la posición 2 sin perder los datos. En la línea 3 se toma el antiguo valor de la posición 0, en estos momentos dentro de la variable temp, y se introduce en la posición 2.

17.2 Ordenamiento Por Selección

El ordenamiento por selección empieza por el principio de la lista. Entonces, el código escanea el resto de la lista en búsqueda del valor más pequeño. Éste es llevado al principio. Luego, el código se mueve hacia el siguiente número más pequeño. Y así sucesivamente. El proceso lo podemos observar gráficamente en la Figura 17.4.

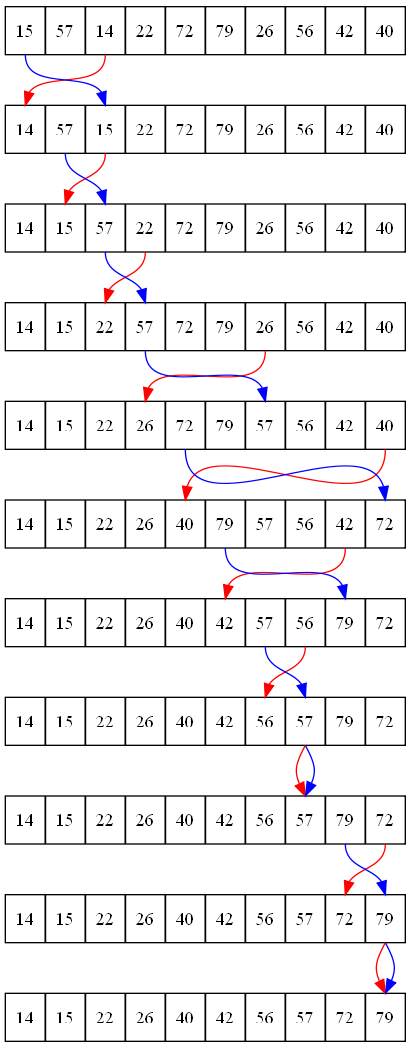
El código para realizar un ordenamiento por selección implica dos bucles anidados. El bucle exterior rastrea la posición donde el código quiere colocar el valor más pequeño. El bucle interior empieza por la ubicación actual y escanea hacia la derecha, buscando el valor más pequeño. Cuando lo encuentra tiene lugar el intercambio.

# Ordenamiento por selección
def ordenamiento_porseleccion(lista):

    # Itera por todo el array
    for pos_actual in range(len(mi_lista)):
	    # Encuentra la posición del valor más pequeño
	    # Empieza por la posición actual
        pos_min = pos_actual

        # Escanea de izquierda a derecha (hasta el final de la lista)
        for escan_pos in range(pos_actual+1, len(mi_lista)):

            # Es ésta la posición más pequeña?
            if mi_lista[escan_pos] < mi_lista[pos_min]:

                # Si lo es, la marcamos como la más pequeña
                pos_min = escan_pos

        # intercambia los dos valores
        temp = mi_lista[pos_min]
        mi_lista[pos_min] = mi_lista[pos_actual]
        mi_lista[pos_actual] = temp

El bucle exterior siempre iterará $n$ veces. El bucle interior iterará $n/2$ veces. Esto ocurrirá siempre sin importar si la lista está en orden o no. La eficiencia del bucle puede mejorarse si comprobamos si los valores para pos_min y pos_actual son iguales antes de la línea 16. Si ambos son iguales no hay necesidad de realizar las tres líneas del código de intercambio.

Usaremos el siguiente código para comprobar el funcionamiento del algoritmo anterior. La primera función imprimirá la lista. Las siguientes líneas crearán, una lista de números aleatorios, los imprimirán, ordenarán y por último, volverá a imprimirlos. En la línea 5, la sentencia print ordenará los números hacia la derecha para facilitar su lectura. La sintaxis para los formatos de impresión la veremos en el Capítulo 20.

# Pega antes del siguiente código el algoritmo de ordenamiento por selección e introduce import random

def print_lista(mi_lista):
    for item in mi_lista:
        print("{:3}".format(item), end="")
    print()

# Creamos una lista con números aleatorios
mi_lista = []
for i in range(10):
    lista.append(random.randrange(100))

# Intentamos el ordenamiento
print_lista(mi_lista)
ordenamiento_porseleccion(mi_lista)
print_lista(mi_lista)

Observa una una animación del ordenamiento por selección en:
http://www.sorting-algorithms.com/selection-sort

Para una demostración muy particular de este algoritmo, busca en Youtube el término “selection sort dance” o utiliza este enlace:
http://youtu.be/Ns4TPTC8whw

Puedes iterar a través del código usando http://pythontutor.com.

17.3 Ordenamiento Por Inserción

El ordenamiento por inserción se parece al de selección por la forma en la que funciona el bucle exterior. El ordenamiento por selección empieza por la izquierda del array y va trabajando hacia su derecha. La diferencia estriba en que no selecciona el elemento más pequeño para hacer el intercambio, lo que hace es trasladar hacia la izquierda cada elemento más pequeño que va encontrando en su camino. Lo podemos ver gráficamente en la Figura 17.5.

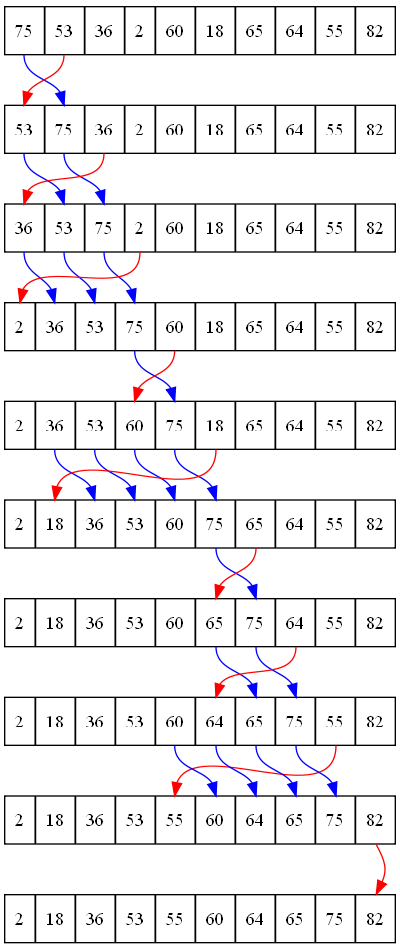
Este ordenamiento divide la lista en dos secciones; la mitad “ordenada” y la mitad “desordenada”. En cada vuelta del bucle exterior, el algoritmo recogerá el siguiente elemento desordenado y lo insertará en la lista.

En el siguiente código, la variable pos_clave señala la frontera entre las porciones ordenadas y desordenadas de la lista. El algoritmo escanea hacia la izquierda de pos_clave usando la variable escan_pos. Debemos observar que en el ordenamiento por inserción, escan_pos desciende hacia la izquierda en lugar de hacerlo hacia la derecha. Cada celda que es mayor a valor_clave es desplazada una posición hacia arriba (a la derecha).

Cuando el bucle encuentra una celda más pequeña que valor_clave, se detiene y coloca valor_clave a su izquierda.

El bucle exterior, en un ordenamiento por inserción, se ejecutará $n$ veces. El bucle interior lo hará, de media, $n/2$ veces si fue creado aleatoriamente. Por el contrario, si el bucle ha sido ordenado en parte previamente, el interior no iterará muchas veces, siendo el tiempo de ordenamiento cercano a $n$.

# Ordenamiento por inserción
def ordenamiento_porinsercion(mi_lista):

    # Empieza en el segundo elemento (posición 1)
    # Usa este elemento para insertarlo en la
    # lista.
    for pos_clave in range(1, len(mi_lista)):

        # Obtiene el valor del elemento a insertar
        valor_clave = mi_lista[pos_clave]

        # Escanea desde la derecha hacia la izquierda (principio de la lista)
        escan_pos = pos_clave - 1

        # Itera cada elemento , trasladándolo hacia arriba hasta que
        # alcanza su ubicación
        while (escan_pos >= 0) and (mi_lista[escan_pos] > valor_clave):
            mi_lista[escan_pos + 1] = mi_lista[escan_pos]
            escan_pos = escan_pos - 1

        # Introducimos la clave en la ubicación correcta
        mi_lista[escan_pos + 1] = valor_clave

Observa una una animación del ordenamiento por inserción en:
http://www.sorting-algorithms.com/insertion-sort

Para una demostración muy particular de este algoritmo, busca en Youtube el término “insertion sort dance” o utiliza este enlace:
http://youtu.be/ROalU379l3U

Puedes iterar a través del código usando http://pythontutor.com.

17.3.1 Test

Haz click para ir al Test.

17.3.2 Ejercicios

Haz click para ir a los Ejercicios.

You are not logged in. Log in here and track your progress.