Chapter 18: Sorting

Binary searches only work on lists that are in order. So how do programs get a list in order? How does a program sort a list of items when the user clicks a column heading, or otherwise needs something sorted?

There are several algorithms that do this. The two easiest algorithms for sorting are the selection sort and the insertion sort. Other sorting algorithms exist as well, such as the shell, merge, heap, and quick sorts.

The best way to get an idea on how these sorts work is to watch them. To see common sorting algorithms in action visit this excellent website:
http://www.sorting-algorithms.com

Each sort has advantages and disadvantages. Some sort a list quickly if the list is almost in order to begin with. Some sort a list quickly if the list is in a completely random order. Other lists sort fast, but take more memory. Understanding how sorts work is important in selecting the proper sort for your program.

18.1 Swapping Values

Before learning to sort, we need to learn how to swap values between two variables. This is a common operation in many sorting algorithms. Suppose a program has a list that looks like the following:

list = [15,57,14,33,72,79,26,56,42,40]

The developer wants to swap positions 0 and 2, which contain the numbers 15 and 14 respectively. See Figure 18.1.

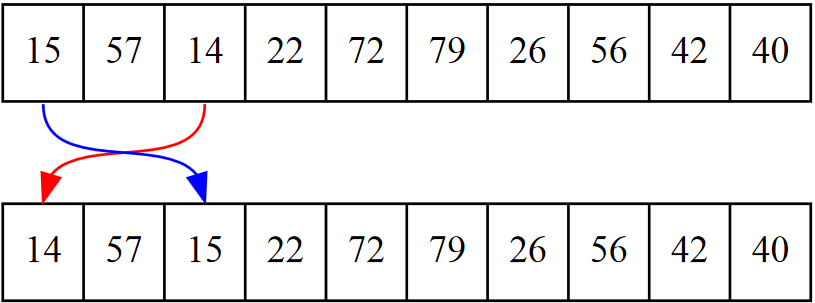
A first attempt at writing this code might look something like this:

list[0] = list[2]
list[2] = list[0]

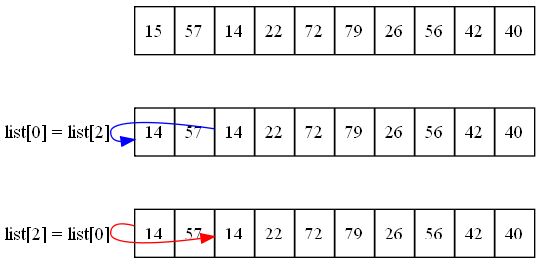
See Figure 18.2 to get an idea on what would happen. This clearly does not work. The first assignment list[0] = list[2] causes the value 15 that exists in position 0 to be overwritten with the 14 in position 2 and irretrievably lost. The next line with list[2] = list[0] just copies the 14 back to cell 2 which already has a 14.

To fix this problem, swapping values in an array should be done in three steps. It is necessary to create a temporary variable to hold a value during the swap operation. See Figure 18.3. The code to do the swap looks like the following:

temp = list[0]
list[0] = list[2]
list[2] = temp

The first line copies the value of position 0 into the temp variable. This allows the code to write over position 0 with the value in position 2 without data being lost. The final line takes the old value of position 0, currently held in the temp variable, and places it in position 2.

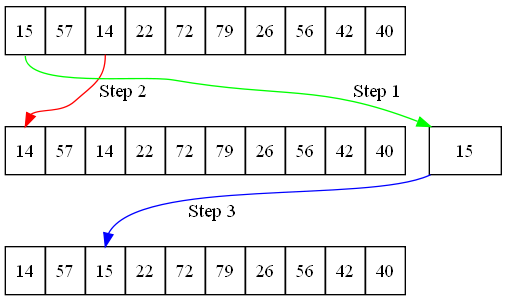
18.2 Selection Sort

The selection sort starts at the beginning of the list. Then code next scans the rest of the list to find the smallest number. The smallest number is swapped into location. The code then moves on to the next number. Graphically, the sort looks like Figure 18.4.

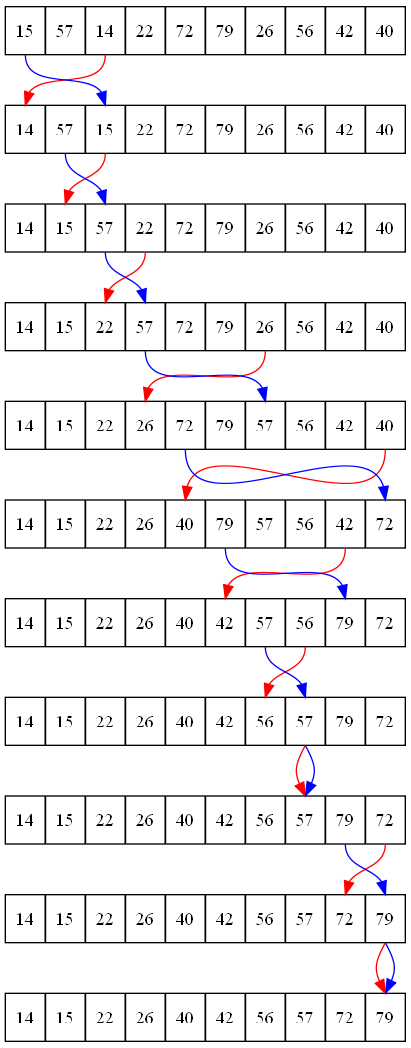
The code for a selection sort involves two nested loops. The outside loop tracks the current position that the code wants to swap the smallest value into. The inside loop starts at the current location and scans to the right in search of the smallest value. When it finds the smallest value, the swap takes place.

# The selection sort
def selection_sort(list):

    # Loop through the entire array
    for curPos in range( len(list) ):
	    # Find the position that has the smallest number
	    # Start with the current position
        minPos = curPos
        
        # Scan left
        for scanPos in range(curPos+1, len(list) ):
        
            # Is this position smallest?
            if list[scanPos] < list[minPos]:
            
                # It is, mark this position as the smallest
                minPos = scanPos
        
        # Swap the two values
        temp = list[minPos]
        list[minPos] = list[curPos]
        list[curPos] = temp

The outside loop will always run $n$ times. The inside loop will run $n/2$ times. This will be the case regardless if the list is in order or not. The loops efficiency may be improved by checking if minPos and curPos are equal before line 16. If those variables are equal, there is no need to do the three lines of swap code.

In order to test the selection sort code above, the following code may be used. The first function will print out the list. The next code will create a list of random numbers, print it, sort it, and then print it again. On line 3 the print statement right-aligns the numbers to make the column of numbers easier to read. Formatting print statements will be covered in Chapter 21.

def print_list(list):
    for item in list:
        print("%3d" % item,end="")
    print()
	
# Create a list of random numbers
list = []
for i in range(10):
    list.append(random.randrange(100))

# Try out the sort
print_list(list)
selection_sort(list)		
print_list(list)

18.3 Insertion Sort

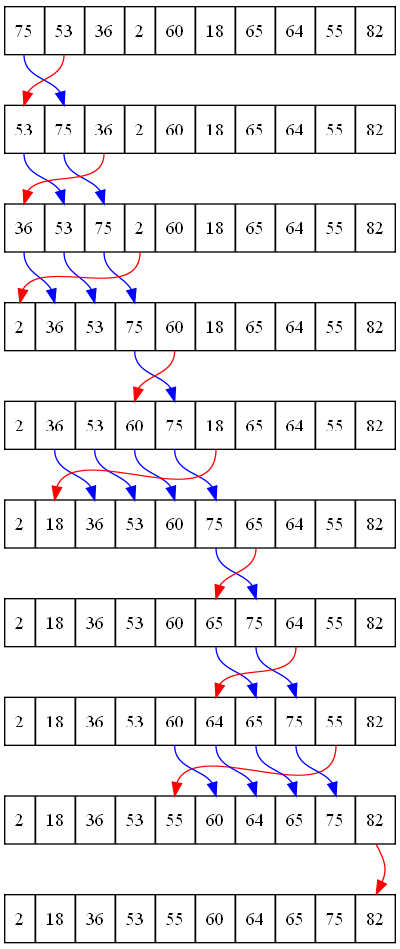
The insertion sort breaks the list into two sections, the “sorted” half and the “unsorted” half. In each round of the outside loop, the algorithm will grab the next unsorted element and insert it into the list.

In the code below, the keyPos marks the boundary between the sorted and unsorted portions of the list. The algorithim scans to the left of keyPos using the variable scanPos. Note that in the insertion short, scanPos goes down to the left, rather than up to the right. Each cell location that is larger than keyValue gets moved up (to the right) one location.

When the loop finds a location smaller than keyValue, it stops and puts keyValue to the left of it.

The outside loop with an insertion sort will run $n$ times. The inside loop will run an average of $n/2$ times if the loop is randomly shuffled. If the loop is close to a sorted loop already, then the inside loop does not run very much, and the sort time is closer to $n$.

def insertion_sort(list):

    # Start at the second element (pos 1).
    # Use this element to insert into the
    # list.
    for keyPos in range(1, len(list)):
    
        # Get the value of the element to insert
        keyValue = list[keyPos]
        
        # Scan to the left
        scanPos = keyPos - 1
        
        # Loop each element, moving them up until
        # we reach the position the 
        while (scanPos >= 0) and (list[scanPos] > keyValue):
            list[scanPos + 1] = list[scanPos]
            scanPos = scanPos - 1
            
        # Everything's been moved out of the way, insert
        # the key into the correct location
        list[scanPos + 	1] = keyValue

18.4 Review Questions

This review is divided into two parts. The second part covers this chapter. The first part covers Chapters 17 and before. Most students find it is a good idea to do some comprehensive review at this point.

Click here for a multiple-choice review quiz.

A video with a full explanation of the answers in the worksheet can be seen [here].

18.4.1 Prior Chapters

1. Write a for loop that will print out a horizontal line of ten asterisks (*).
2. Write two nested for loops that will print a 10x10 box of asterisks.
3. Write Python code that will create an array of 100 zeros.
4. What is the difference between a class and an object?
5. What is the difference between a function and a method?
6. Write a function that prints your favorite number.
7. Call the function that prints your favorite number.
8. Write a function that takes three numbers as parameters and returns the average.
9. Programming classes:
   1. Write code for a class called Ball. Give it attributes for its position, and its velocity.
   2. Create a method called update that will move the ball's position according to its velocity.
   3. Create an instance of the Ball class, set its attributes.
   4. Create a for loop that will call the update method on ball 10 times, and print the ball's position.

18.4.2 Sorting Chapter

10. Write code to swap the values 25 and 40.

    list = [55, 41, 52, 68, 45, 27, 40, 25, 37, 26]
    

11. Write code to swap the values 2 and 27.

    list = [27, 32, 18,  2, 11, 57, 14, 38, 19, 91]
    

12. Why does the following code not work?

    list = [70, 32, 98, 88, 92, 36, 81, 83, 87, 66]
    temp = list[0]
    list[1] = list[0]
    list[0] = temp 
    

13. Show how the numbers in Figure 18.6 are sorted, using the selection sort.

    

14. Show how the numbers in Figure 18.7 are sorted, using the selection sort.

    

15. Show how the numbers in Figure 18.8 are sorted, using the insertion sort.

    

16. Show how the numbers in Figure 18.9 are sorted, using the insertion sort.

    

17. Explain what minPos does in the selection sort.
18. Explain what curPos does in the selection sort.
19. Explain what scanPos does in the selection sort.
20. Explain what keyPos and keyValue are in the insertion sort.
21. Explain scanPos in the insertion sort.
22. Modify the sorts to print the number of times the inside loop is run, and the number of times the outside loop is run.

You are not logged in. Log in here and track your progress.