Chapter 19: Рекурсия

Ребёнок не мог заснуть, поэтому его мама рассказала ему историю о маленьком лягушонке,
  который не мог заснуть, поэтому мама-лягушка рассказала ему историю о маленьком медвежонке,
    который не мог заснуть, поэтому мама-медведица рассказала ему историю о маленькой ласке...
      которая заснула.
    ...и маленький медвежонок заснул;
  ...и маленький лягушонок заснул;
...и ребёнок заснул.

Источник: http://everything2.com/title/recursion

Рекурсия это процесс или объект, который использует самого себя ради собственного определения. Математические закономерности, такие, как факториалы или числа фибоначчи, рекурсивны. Документы, содержащие другие документы, которые, в свою очередь, могут содержать свои документы, рекурсивны. Фрактальные картинки и даже некоторые биологические процессы рекурсивны в своих прицнипах работы.

19.1 Где используется рекурсия?

Документы, такие как интернет страницы, по своей сути рекурсивны. Например, материал приведённый далее является простым веб документом:

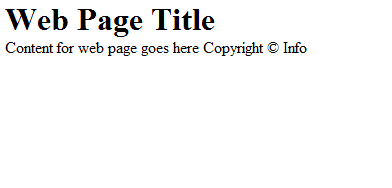
Этот веб документ может содержаться в 'коробке', что может помочь размещению элементов на странице:

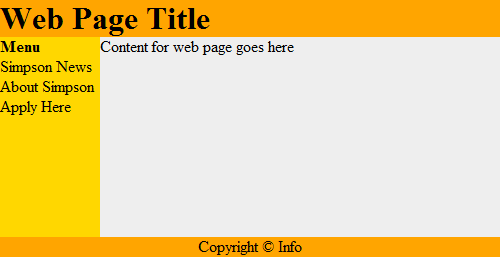
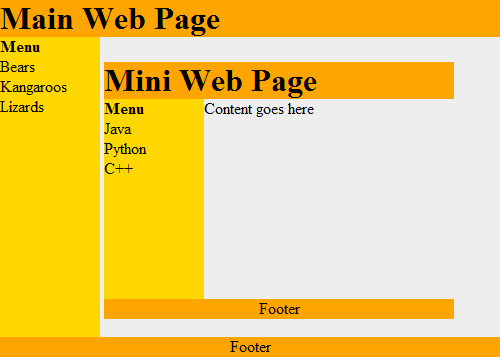
Это работает рекурсивно. Каждая рамка может содержать в себе веб страницу, которая, в свою очередь, может содержать рамку, которая содержит другую веб страницу:

Рекурсивные функции зачастую используются с продвинутыми алгоритмами сортировки, которые будут описаны в другом курсе.

Даже если человек не станет программистом, ему очень важно понимать концепцию рекурсивных систем. Если появляется деловая надобность в рекурсивных структурах таблиц, документах или чем-то ещё, важно знать, как описать такие вещи программисту.

Например, человек может указать, что веб-программе для рецептов потребуется способность поддерживать ингридиенты и инструкции. Человек, знакомый с концепцией рекурсии просто укажет, что каждый ингридиет может сам по себе быть рецептом с другими ингридиентами (которые тоже могут быть рецептами). Вторая система будет значительно более мощной.

19.2 Что есть рекурсия на програмном уровне?

В предыдущих главах, мы использовали функции, вызывающие другие функции. Например:

def f():
    g()
    print("f")

def g():
    print("g")
    
f()

Также, функция может вызывать саму себя. Функция, вызывающая саму себя, использует принцип рекурсии. Например:

def f():
    print("Hello")
	f()

f()

Вышеприведённый пример выведет Hello, а затем снова вызовет функцию f(), которая, в свою очередь, выведет на экран ещё одно Hello и снова вызовет функцию f(). Это будет продолжаться до момента, пока у компьютера не кончится место в стеке. Когда это случится, Python выведет на экран длинную ошибку, которая закончится с:
RuntimeError: maximum recursion depth exceeded

Компьютер говорит, что программист ушёл слишком далеко в своей рекурсии.

19.3 Контроль глубины рекурсии

Для успешного использования рекурсии, нужен способ для предотвращения бесконечного повторного вызова функции. Нижеприведённый пример считает, сколько раз была вызвана функция, а затем использует выражение if для выхода после того, как функция вызвала себя 10 раз.

def f(level): # Вывести наш текущий уровень print("Recursion call, level",level) # Если мы не достигли 10го уровня... if level < 10: # Снова вызовем эту функцию, # прибавив к уровню единицу f(level+1) # Начать рекурсивный вызов на уровне 1 f(1)

Output: Recursion call, level 1 Recursion call, level 2 Recursion call, level 3 Recursion call, level 4 Recursion call, level 5 Recursion call, level 6 Recursion call, level 7 Recursion call, level 8 Recursion call, level 9 Recursion call, level 10

19.4 Рекурсивное вычисление факториала

Любая задача, которую можно решить с помощью рекурсии, решаема и без рекурсии. Некоторые программисты считают, что рекурсивный код проще для понимания.

Вычисление факториала числа - классический пример применения рекурсии. Факториалы полезны в теории вероятности и статистике. Например:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$

Рекурсивно, это может быть описано как:
$n! = \begin{cases} 1 & \text{if } n = 0, \\ n \cdot (n-1)! & \text{if } n > 0. \end{cases}$

Ниже для примера приведены две функции, вычисляющие $n!$. Первая - нерекурсивная. Вторая - рекурсивная.

# Эта программа вычисляет факториал
# БЕЗ использования рекурсии
def factorial_nonrecursive(n):
    answer = 1
    for i in range(2,n+1):
        answer = answer * i
    return answer

# Эта программа вычисляет факториал
# С использованием рекурсии
def factorial_recursive(n):
    if( n == 1 ):
        return n
    else:
        return n * factorial_recursive(n-1)   

Сами по себе функции ничего не делают. Ниже приведён пример, где мы сложили их все вместе. Этот пример также добавляет несколько выражений print() внутри функций, чтобы мы легче могли наблюдать за тем, что происходит,

# Эта программа вычисляет факториал # БЕЗ использования рекурсии def factorial_nonrecursive(n): answer = 1 for i in range(2,n+1): print( i,"*",answer,"=", i*answer) answer = answer * i return answer print("I can calculate a factorial!") user_input = input ("Enter a number:") n = int(user_input) answer = factorial_nonrecursive(n) print (answer) # Эта программа вычисляет факториал # С использованием рекурсии def factorial_recursive(n): if( n == 1 ): return n else: x = factorial_recursive(n-1) print( n, "*", x, "=", n * x ) return n * x print("I can calculate a factorial!") user_input = input ("Enter a number:") n = int(user_input) answer = factorial_recursive(n) print (answer)

Вывод: I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040

19.5 Рекурсивные прямоугольники

Рекурсия прекрасно работает со структурированными документами, который рекурсивны сами по себе. Например, веб документ может содержать таблицу, разделённую на несколько рядов и столбцов для помощи с расположением элементов. Один ряд может быть заголовком, другой - основной частью, третий - нижним колонтитулом. Внутри одной из ячеек таблицы может находится другая таблица. А внутри неё может существовать ещё одна таблица.

Другой пример - электронная почта. Возможно прикрепить письмо одного человека к вашему письму. Но то письмо может уже содержать ещё одно письмо, и т.д.

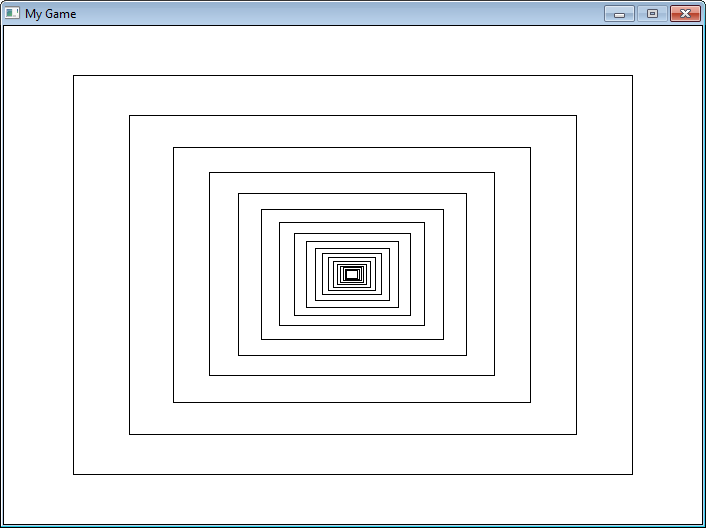
Ниже приведён пример кода pygame, рисующий прямоугольник, а затем рекурсивно продолжающий рисовать прямоугольники внутри него, каждый на 20% меньше предыдущего. Посмотрите внимательнее на рекурсивные вызовы в функции recursive_draw().

# Sample Python/Pygame Programs
# Simpson College Computer Science
# http://programarcadegames.com/
# http://simpson.edu/computer-science/
 
import pygame
 
# Задать цвета
black    = (   0,   0,   0)
white    = ( 255, 255, 255)
green    = (   0, 255,   0)
red      = ( 255,   0,   0)
 
def recursive_draw(x,y,width,height):
    # Нарисовать прямоугольник
    pygame.draw.rect(screen,black,[x,y,width,height],1)

    # Является ли прямоугольник достаточно широким, 
	#　чтобы нарисовать внутри его ещё один?
    if( width > 14 ):
        # Уменьшить масштаб
        x += width * .1
        y += height * .1
        width *= .8
        height *= .8
        # Рекурсивно нарисовать ещё один
        recursive_draw(x,y,width,height)
    
pygame.init()
  
# Задать высоту и ширину экрана
size=[700,500]
screen=pygame.display.set_mode(size)
 
pygame.display.set_caption("My Game")
 
# Идти по циклу до тех пор, пока пользователь не нажмёт кнопку "закрыть"
done=False
 
# Управляет, как быстро обновляется экран
clock=pygame.time.Clock()
 
# -------- Основной цикл программы -----------
while done==False:
    for event in pygame.event.get(): # Пользователь что-то сделал
        if event.type == pygame.QUIT: # Если пользователь нажал на кнопку закрытия
            done=True # Отметить, что мы выходим
 
    # Установить фон экрана
    screen.fill(white)
 
    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    recursive_draw(0,0,700,500)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT
     
    # Ограничить до 20 кадров в секунду
    clock.tick(20)
 
    # Обновить экран тем, что мы нарисовали
    pygame.display.flip()
     
# Будьте дружелюбны к IDLE. Если вы забудете эту строку,
# программа зависнет на выходе
pygame.quit ()

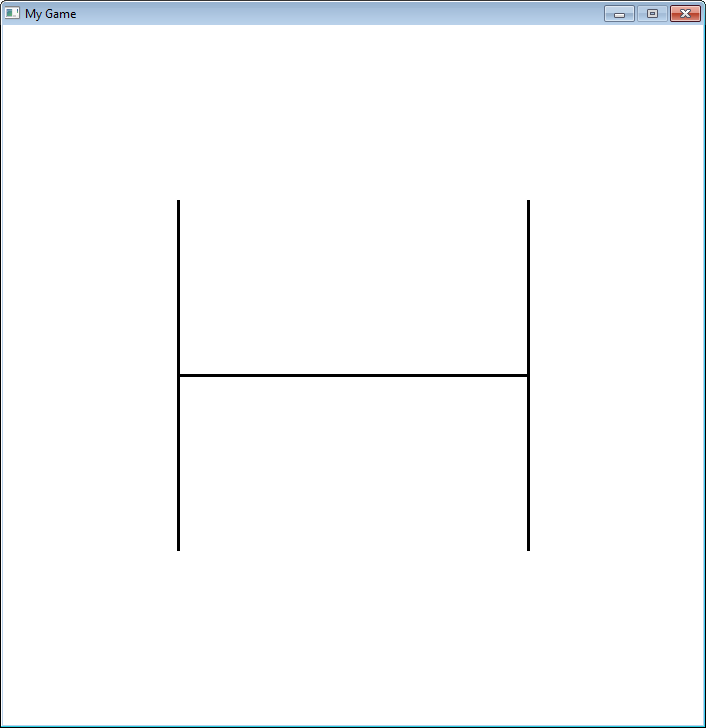
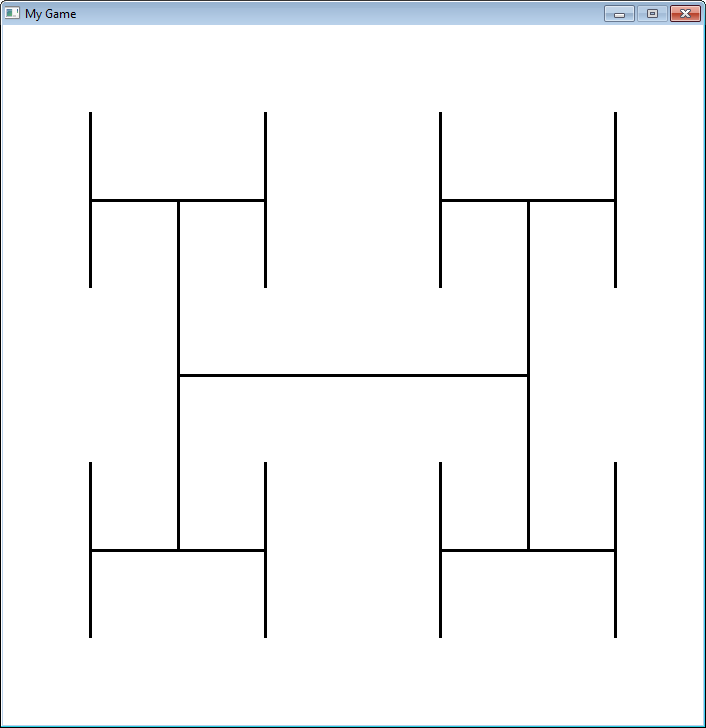
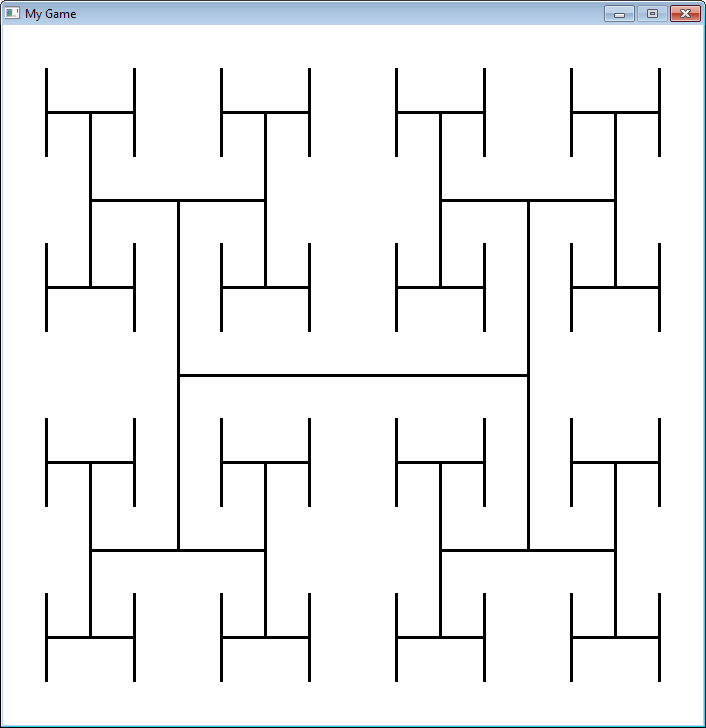
19.6 Фракталы

Фракталы задаются рекурсивно. Вот простой фрактал, показывающий, как он меняется в зависимости от “глубины” рекурсии.

# Sample Python/Pygame Programs
# Simpson College Computer Science
# http://programarcadegames.com/
# http://simpson.edu/computer-science/
 
import pygame
 
# Задать цвета
black    = (   0,   0,   0)
white    = ( 255, 255, 255)
green    = (   0, 255,   0)
red      = ( 255,   0,   0)
 
def recursive_draw(x,y,width,height,count):

    pygame.draw.line(screen,black,[x+width*.25,height//2+y],[x+width*.75,height//2+y],3)
    pygame.draw.line(screen,black,[x+width*.25,(height*.5)//2+y],[x+width*.25,(height*1.5)//2+y],3)
    pygame.draw.line(screen,black,[x+width*.75,(height*.5)//2+y],[x+width*.75,(height*1.5)//2+y],3)

    if count > 0:
        count -= 1
        # Верхний левый
        recursive_draw(x,y,                    width//2,height//2,count)
        # Верхний правый
        recursive_draw(x+width//2,y,           width//2,height//2,count)
        # Нижний левый
        recursive_draw(x,y+width//2,           width//2,height//2,count)
        # Нижний правый
        recursive_draw(x+width//2,y+width//2,  width//2,height//2,count)
    
    
pygame.init()
  
# Задать высоту и ширину экрана
size=[700,700]
screen=pygame.display.set_mode(size)
 
pygame.display.set_caption("My Game")
 
# Идти по циклу до тех пор, пока пользователь не нажмёт кнопку "закрыть"
done=False
 
# Управляет, как быстро обновляется экран
clock=pygame.time.Clock()
 
# -------- Main Program Loop -----------
while done==False:
    for event in pygame.event.get(): # Пользователь что-то сделал
        if event.type == pygame.QUIT: # Если пользователь нажал на кнопку закрытия
            done=True # Отметить, что мы выходим
 
    # Установить фон экрана
    screen.fill(white)
 
    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    fractal_level=3
    recursive_draw(0,0,700,700,fractal_level)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT
     
    # Ограничить до 20 кадров в секунду
    clock.tick(20)
 
    # Обновить экран тем, что мы нарисовали
    pygame.display.flip()
     
# Будьте дружелюбны к IDLE. Если вы забудете эту строку,
# программа зависнет на выходе
pygame.quit ()

Рекурсия также может быть использована в бинарном поиске. Вот не-рекурсивный бинарный поиск из главы 17:

def binary_search_nonrecursive(search_list,key):
    lower_bound = 0
    upper_bound = len(search_list)-1
    found = False
    while lower_bound < upper_bound and found == False:
        middle_pos = (int) ((lower_bound+upper_bound) / 2)
        if search_list[middle_pos] < key:
            lower_bound = middle_pos+1
        elif list[middle_pos] > key:
            upper_bound = middle_pos
        else:
            found = True
     
    if found:
        print( "The name is at position",middle_pos)
    else:
        print( "The name was not in the list." )
        
binary_search_nonrecursive(name_list,"Morgiana the Shrew")

Вот тот же самый поиск, написаный с применением рекурсии:

def binary_search_recursive(search_list,key, lower_bound, upper_bound):
    middle_pos = (int) ((lower_bound+upper_bound) / 2)
    if search_list[middle_pos] < key:
        binary_search_recursive(search_list,key, middle_pos+1, upper_bound)
    elif search_list[middle_pos] > key:
        binary_search_recursive(search_list,key, lower_bound, middle_pos )
    else:
        print("Found at position",middle_pos)
        
lower_bound = 0
upper_bound = len(name_list)-1
binary_search_recursive(name_list,"Morgiana the Shrew",lower_bound,upper_bound)

19.7 Проверка пройденного

1. “Для понимания рекурсии, нужно сначала понять рекурсию.” Объясните шутку.
2. Два зеркала поставлены друг напротив друга. Объясните, как их отражение демонстрирует принцип рекурсии.
3. Объясните как мульти-уровневый маркетинг использует рекурсию.
4. Объясните как функция открывания полей в классической игре сапёр может быть сделана рекурсивно.
5. Объясните, как можно найти выход из лабиринта с помощью рекурсии.
6. Используя браузер Chrome, создайте свой скриншот на: http://juliamap.googlelabs.com. Используйте alt-PrtScr для захвата картинки и вставьте её в ворд-файл.
   (Просто так: ознакомьтесь с этим и этим тоже.)
7. Напишите рекурсивную функцию f(n), берущую значение n и возвращающую значение f, принимая во внимание следующую дефиницию:
   $f_{n} = \begin{cases} 6 & \text{if } f = 1, \\ \frac{1}{2}f_{n-1}+4 & \text{if } f > 1. \end{cases}$
   Затем напишите цикл for, выводящий ответы для n от 1 до 10. Оно должно выглядеть следующим образом:

   n= 1 , a= 6
   n= 2 , a= 7.0
   n= 3 , a= 7.5
   n= 4 , a= 7.75
   n= 5 , a= 7.875
   n= 6 , a= 7.9375
   n= 7 , a= 7.96875
   n= 8 , a= 7.984375
   n= 9 , a= 7.9921875
   n= 10 , a= 7.99609375
   

8. Напишите рекурсивный код, выводящий первые 10 чисел из последовательности: $f_{n} = \begin{cases} 1 & \text{if } f = 1, \\ 1 & \text{if } f = 2, \\ f(n-1)+f(n-2) & \text{if } f > 2. \end{cases}$
   

You are not logged in. Log in here and track your progress.