Chapter 19: Rekurzió (önhívás)

Van egy gyerek, aki nem tud aludni, így az anyukája mesél neki egy mesét egy kis békáról,
   aki nem tud aludni, így az anyukája mesél neki egy mesét egy medvebocsról,
    aki nem tud aludni, így a bocs anyukája mesél neki egy mesét egy kis menyétről...
      aki elaludt.
    ...és így a medvebocs elaludt;
  ...és így a kis béka is elaludt;
...és a kisgyerek is elaludt.
(Forrás: http://everything2.com/title/recursion)

A rekurzió egy objektum, vagy folyamat, ami saját maga által van meghatározva. A matematikai minták, mint amilyen a faktoriális, vagy a Fibonacci sorozat rekurzív. Azok a dokumentumok, amik más dokumentumokat tartalmaznak, és azok is más doksikat tartalmazhatnak, szintén rekuzívak. Fraktálos képek, és még a biológiai folyamatok is rekurzívak működésük szerint.

19.1 Hol használják a rekurziót??

A dokumentumok, mint amilyen a weboldalak, természetüknél fogva rekurzívak. Például, ezen az ábrán láthatsz egy ilyen web dokumentumot: 19.1 .

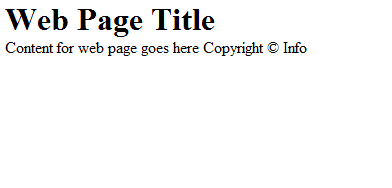
Ez a weboldal magába foglal egy "ládikát", ami segíti az oldalt a rétegek létrehozásában. Ábra: 19.2.

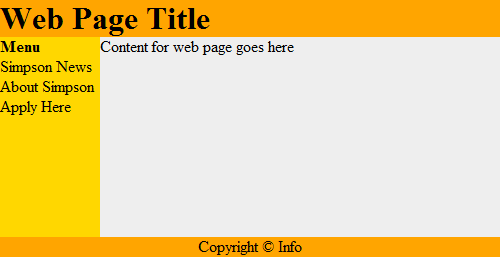
Ez rekurzívan működik. Minden ládikában van egy weboldal, aminek lehet egy újabb ládikája, ami újabb weboldalt foglalhat magába. 19.3.

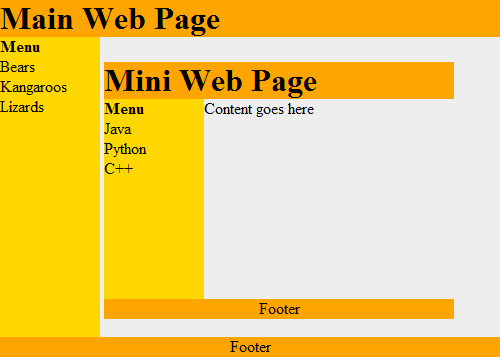
A rekurzív függvények gyakran használva vannak jobb keresésnél és sorbarendező algoritmusoknál. Be fogunk mutatni egy párat ezekből, és ha felveszel majd egy adatstruktúrák kurzust akkor még többel is találkozhatsz.

Még ha valaki nem is lesz programozó, akkor is fontos megértenie a rekurzív rendszerek lényegét. Ha olyan üzletben vesz részt, ami rekurzív táblázatokat kíván, vagy dokumentumokat, vagy bármi mást, akkor fontos, hogy tudja, hogyan kérje majd ezt a programozótól.

Például, valaki szeretné meghatározni egy webprogramban, hogy a receptek milyen hozzávalókkal készülnek. A rekurzív gondolkodásban jártas programozó szerint, minden hozzávaló lehet recept más hozzávalókkal együtt. Ez egy hatékony módszer.

19.2 Hogyan kódoljuk a rekurziót?

Az előző fejezetekben, olyan függvényeket használtunk, amik más függvényeket használtak. Például:

def f():
    g()
    print("f")

def g():
    print("g")
    
f()

Lehetőség van rá, hogy egy függvény saját magát hívja. Ha egy függvény magát is meghívhatja, amikor őt meghívják, akkor az a függvény rekurzív. Például:

def f():
    print("Hello")
    f()

f()

A fenti példa ki fogja írni, hogy Hello, és azután újra meghívja az f() függvényt. Aminek hatására, újra kiírja, hogy Hello, és újra meghívja az f() függvényt. Ez egészen addig fog folytatódni, amíg a számítógép ki nem fogy az úgynevezett tárhelyből. Amikor ez történik, akkor a Python egy hosszú hibaüzenetet küld, ami ezzel ér véget:
RuntimeError: maximum recursion depth exceeded (Futási idő hiba: maximum rekurziós mélység elérve)

A számítógép azt üzeni neked, a programozónak, hogy túl mélyre hatoltál a nyúlüregben.

19.3 Rekurziós mélység vezérlése

Ahhoz, hogy sikeresen használjuk a rekurziót, szükségünk van egy módszerre, ami meggátolja azt, hogy újra és újra hívja meg magát, végtelenszer. Az alábbi példa, megszámolja, hogy mennyiszer képes meghívni saját magát. Ehhez használ egy if parancsot, hogy kilépjen, amikor tízszer végrehajtódott.

def f(level):
    # írjuk ki a szintet, ahol éppen tartunk
    print("Recursion call, level",level)
    # ha nem érjük el a tizedik szintet...
    if level < 10:
        # hívjuk meg a függvényt megint
        # és adjunk egy szintet neki
        f(level+1)

#Indítsuk újra a rekurzív hívást az első szintről 
f(1)

Recursion call, level 1
Recursion call, level 2
Recursion call, level 3
Recursion call, level 4
Recursion call, level 5
Recursion call, level 6
Recursion call, level 7
Recursion call, level 8
Recursion call, level 9
Recursion call, level 10

19.4 Rekurziós faktoriális számítás

Bármely kód, ami rekurzív lehet, használható rekurzió nélkül is. Némely programozó úgy érzi, hogy a rekurzív kódot könnyebb megérteni.

Egy szám faktoriálisát kiszámítani egy klasszikus példa a rekurzió használatára. A faktoriálisok hasznosak a valószínűségszámítás és a statisztika szempontjából. Például:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$

Rekurzívan így írható le:
$n! = \begin{cases} 1 & \text{if } n = 0, \\ n \cdot (n-1)! & \text{if } n > 0. \end{cases}$

Alább van két példafüggvény, ami kiszámítja az $n!$-t. Az első nem rekurzív, a második már rekurzív.

# Ez a program egy faktoriálist számít ki
# rekurzió használata NÉLKÜL
def factorial_nonrecursive(n):
    answer = 1
    for i in range(2,n+1):
        answer = answer * i
    return answer

# Ez a program egy faktoriálist számít ki, 
# rekurzióval
def factorial_recursive(n):
    if( n == 1 ):
        return n
    else:
        return n * factorial_recursive(n-1)   

A függvények nem tesznek semmit saját magukkal. A lenti példában mi az összes tudást egyberakjuk. Ez a példa tartalmaz még print parancsokat is, így láthatjuk azt is, ami történik.

# Ez a program faktoriálist számít
# rekurzió NÉLKÜL

def factorial_nonrecursive(n):
    answer = 1
    for i in range(2,n+1):
        print( i,"*",answer,"=", i*answer)
        answer = answer * i
    return answer

print("I can calculate a factorial!")
user_input = input ("Enter a number:")
n = int(user_input)
answer = factorial_nonrecursive(n)
print (answer)

# Ez a program faktoriálist számít
# rekurzióval

def factorial_recursive(n):
    if( n == 1 ):
        return n
    else:
        x = factorial_recursive(n-1)
        print( n, "*", x, "=", n * x )
        return n * x
    
print("I can calculate a factorial!")
user_input = input ("Enter a number:")
n = int(user_input)
answer = factorial_recursive(n)
print (answer)

I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040
I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040

19.5 Rekurzív téglalapok

A rekurzió nagyszerűen dolgozik strukturált dokumentumokkal, amik maguk is rekurzívak. Például, egy web dokumentumban a táblázat meg van osztva sorra és oszlopra, ami segít a rétegek kialakításában. Egy sor lehet fejléc, a másik a dokumentum teste, míg az utolsó lehet a lábléc. A táblázat celláiban lehet másik táblázat. És ezekben is lehet még egy táblázat.

Másik jó példa az e-mail. Lehetséges hozzácsatolni másik személy e-mailjét a te e-mailedhez. De az az e-mail is tartalmazhat már más, csatolt e-maileket. És így tovább.

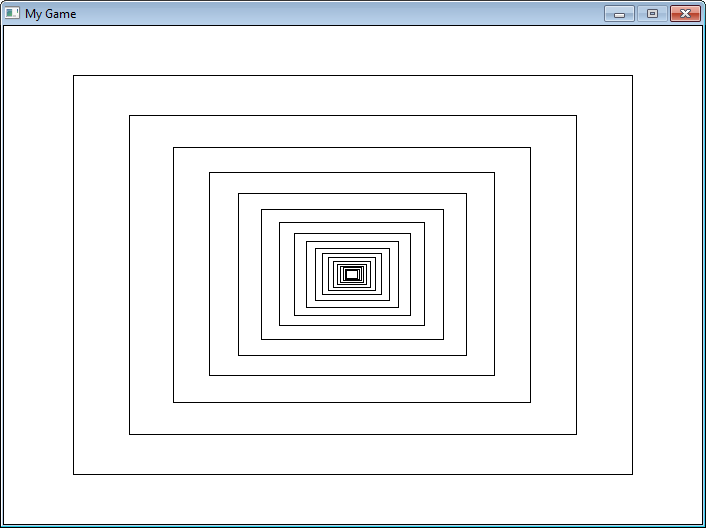
Láthatjuk-e a rekurziót működés közben egy Pygame programunkban? Igen! Az alábbi ábrán 19.4 egy példa program van, ami egy téglalapot rajzol ki, és rekurzívan tartja a téglalapokat egymáson belül. Minden téglalap 20%-kal kisebb mint a szülő téglalap. Vessünk egy pillantást a kódra. Figyeljük meg az apró részleteket is, ahogyan a rekurzív hívás történik a recursive_draw függvényben.

"""
 Recursively draw rectangles.

 Sample Python/Pygame Programs
 Simpson College Computer Science
 http://programarcadegames.com/
 http://simpson.edu/computer-science/

"""
import pygame

# Colors
BLACK = (0, 0, 0)
WHITE = (255, 255, 255)


def recursive_draw(x, y, width, height):
    """ Recursive rectangle function. """
    pygame.draw.rect(screen, BLACK,
                     [x, y, width, height],
                     1)

    # Is the rectangle wide enough to draw again?
    if(width > 14):
        # Scale down
        x += width * .1
        y += height * .1
        width *= .8
        height *= .8
        # Recursively draw again
        recursive_draw(x, y, width, height)

pygame.init()

# Set the height and width of the screen
size = [700, 500]
screen = pygame.display.set_mode(size)

pygame.display.set_caption("My Game")

# Loop until the user clicks the close button.
done = False

# Used to manage how fast the screen updates
clock = pygame.time.Clock()

# -------- Main Program Loop -----------
while not done:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True

    # Set the screen background
    screen.fill(WHITE)

    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    recursive_draw(0, 0, 700, 500)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT

    # Go ahead and update the screen with what we've drawn.
    pygame.display.flip()

    # Limit to 60 frames per second
    clock.tick(60)

# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()

19.6 Fraktálok

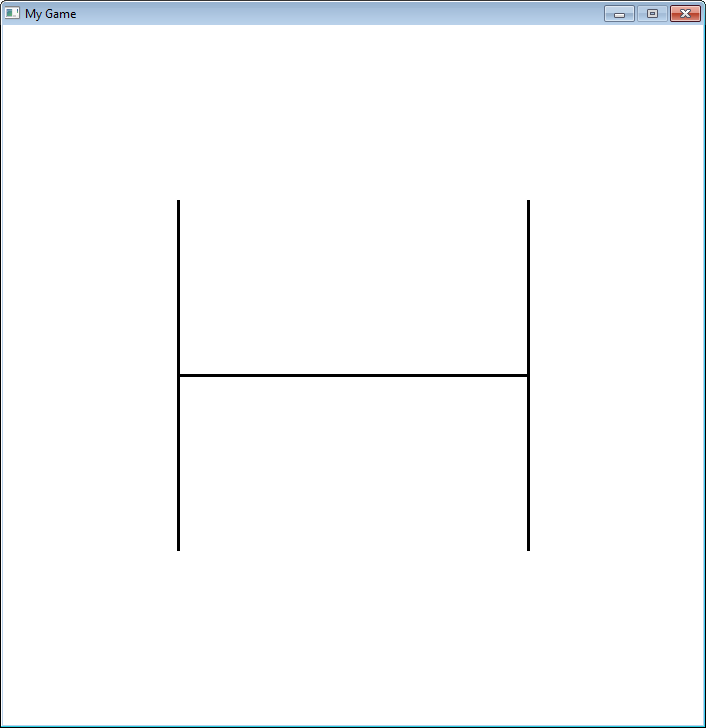
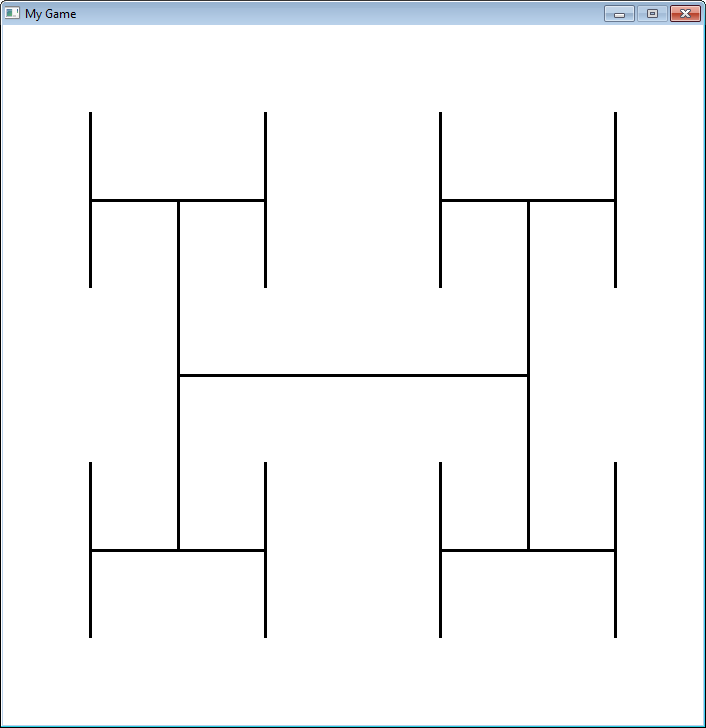
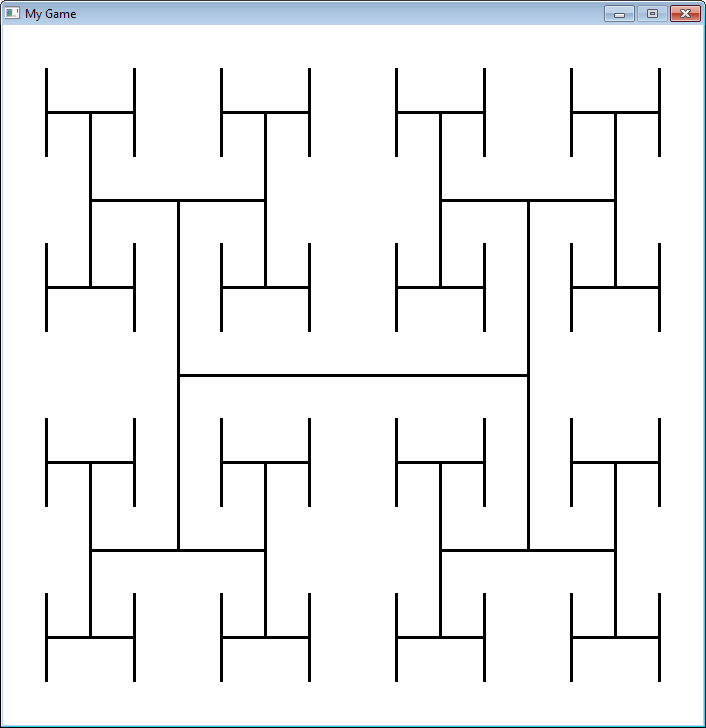
A fraktálokat rekurzívan definiáltuk, Itt egy nagyon egyszerű fraktál, ami azt szemlélteti, hogy hogyan változik, amikor egyre mélyebb rekurzióvá válik.

"""
 Sample fractal using recursion.

 Sample Python/Pygame Programs
 Simpson College Computer Science
 http://programarcadegames.com/
 http://simpson.edu/computer-science/
"""

import pygame

# Define some colors
black = (0, 0, 0)
white = (255, 255, 255)
green = (0, 255, 0)
red = (255, 0, 0)


def recursive_draw(x, y, width, height, count):
    # Draw the rectangle
    # pygame.draw.rect(screen,black,[x,y,width,height],1)
    pygame.draw.line(screen,
                     black,
                     [x + width*.25, height // 2 + y],
                     [x + width*.75, height // 2 + y],
                     3)
    pygame.draw.line(screen,
                     black,
                     [x + width * .25, (height * .5) // 2 + y],
                     [x + width * .25,  (height * 1.5) // 2 + y],
                     3)
    pygame.draw.line(screen,
                     black,
                     [x + width * .75, (height * .5) // 2 + y],
                     [x + width * .75, (height * 1.5) // 2 + y],
                     3)

    if count > 0:
        count -= 1
        # Top left
        recursive_draw(x, y, width // 2, height // 2, count)
        # Top right
        recursive_draw(x + width // 2, y, width // 2, height // 2, count)
        # Bottom left
        recursive_draw(x, y + width // 2, width // 2, height // 2, count)
        # Bottom right
        recursive_draw(x + width // 2, y + width // 2, width // 2, height // 2, count)


pygame.init()

# Set the height and width of the screen
size = [700, 700]
screen = pygame.display.set_mode(size)

pygame.display.set_caption("My Game")

# Loop until the user clicks the close button.
done = False

# Used to manage how fast the screen updates
clock = pygame.time.Clock()

# -------- Main Program Loop -----------
while not done:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True

    # Set the screen background
    screen.fill(white)

    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    fractal_level = 3
    recursive_draw(0, 0, 700, 700, fractal_level)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT

    # Go ahead and update the screen with what we've drawn.
    pygame.display.flip()

    # Limit to 20 frames per second
    clock.tick(20)

# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()

19.7 Rekurzív bináris keresés

A rekurziót lehet még bináris keresésre is használni. Itt van egy nem-rekurzív bináris keresés a 17-dik fejezetből:

def binary_search_nonrecursive(search_list,key):
    lower_bound = 0
    upper_bound = len(search_list)-1
    found = False
    while lower_bound < upper_bound and found == False:
        middle_pos = (lower_bound+upper_bound) // 2
        if search_list[middle_pos] < key:
            lower_bound = middle_pos+1
        elif list[middle_pos] > key:
            upper_bound = middle_pos
        else:
            found = True
     
    if found:
        print( "The name is at position",middle_pos)
    else:
        print( "The name was not in the list." )
        
binary_search_nonrecursive(name_list,"Morgiana the Shrew")

Ez pedig ugyanaz a bináris keresés, amit rekurzívan írtunk meg:

def binary_search_recursive(search_list,key, lower_bound, upper_bound):
    middle_pos = (lower_bound+upper_bound) // 2
    if search_list[middle_pos] < key:
        binary_search_recursive(search_list,
                                key, 
                                middle_pos+1, 
                                upper_bound)
    elif search_list[middle_pos] > key:
        binary_search_recursive(search_list,
                                key,
                                lower_bound, 
                                middle_pos )
    else:
        print("Found at position", middle_pos)
        
lower_bound = 0
upper_bound = len(name_list)-1
binary_search_recursive(name_list,
                        "Morgiana the Shrew",
                        lower_bound,
                        upper_bound)

19.8 Áttekintés

19.8.1 Feladatlap

Click here for the chapter worksheet.

You are not logged in. Log in here and track your progress.