Chapter 19: Rekursio

Pieni lapsi ei saa unta, joten hänen äitinsä kertoo hänelle sadun pikku sammakosta,
  joka ei saa nukuttua, joten sammakkoäiti kertoo hänelle sadun pienestä karhusta,
    joka ei saa nukuttua, joten hänen äitinsä kertoo hänelle sadun pienestä lumikosta...
      joka nukahtaa sikeään uneen.
    ...ja pikku karhu nukahtaa;
  ...ja pieni sammakko nukahtaa;
...ja pikku lapsi nukahtaa.
(Tekstin alkuperäinen lähde, josta käännetty: http://everything2.com/title/recursion)

Rekursio on ohjelmointitekniikka, jossa ongelman ratkaisussa algoritmia itseään kutsutaan. Matemaattiset tehtävät kuten kertoman laskeminen ja Fibonaccin lukujono ovat ratkaistavissa rekursiivisesti. Dokumentit, jotka voivat sisältää toisia dokumentteja ja tämä sisältää edelleen dokumentteja, ovat rekursiivisia. Fraktaalit (toistuvat kuviot) ja tietyt biologiaan liittyvät tapahtumat ovat toiminnaltaan rekursiivisia.

19.1 Missä rekursiota voidaan käyttää?

Web-sivut ovat tietyllä tapaa rekursiivisia. Esimerkkinä kuvassa 19.1 on esitettynä web-dokumentti.

Web-dokumentti voidaan sijoittaa “laatikkoon,” joka saa sivun asettelun helpommaksi. Katso kuva 19.2.

Tämä toimii rekursiivisesti. Jokainen laatikko voi sisältää web-dokumentin, joka voi sisältää toisen web-dokumentin. Katso tämän havainnollistaminen kuvassa 19.3.

Rekursiivisia algoritmeja käytetään edistyneissä haku- ja lajittelualgoritmeissa. Katsotaan tässä muutama esimerkki.

Rekursiivisen ratkaisun periaatteen tuntemisesta on hyötyä muillekin kuin ohjelmoijille. Esimerkiksi liike-elämässä käytetään rekursiivisia taulukointeja, dokumentteja, yms. ja näiden toimenpiteiden määrittäminen rekursiivisesti on hyvä hallita.

Esimerkiksi, websovellus tarvitsee reseptien tulostamiseen ominaisuuden, jossa reseptiin saadaan aineosat ja määrät. Rekursiivisesti tässä voidaan ajatella, että aineosat ovat sinänsä reseptejä, jossa on ainesosia ja määriä.

19.2 Miten rekursiivinen koodi kirjoitetaan?

Edellä käsittelimme funktioiden yhteydessä funktioita, jotka kutsuvat toisia funktioita. Esimerkiksi:

def f():
    g()
    print("f")

def g():
    print("g")

f()

Funktio voi kutsua myös itseään. Itseään kutsuvaa funktioita kutsutaan rekursiiviseksi funktioksi. Esimerkiksi:

def f():
    print("Hello")
    f()

f()

Koodi tulostaa Hello ja kutsuu uudelleen itseään, eli f() funktiota. Tämä saa aikaiseksi Hello tulostuksen uudelleen ja taas uuden funktiokutsun f(). Tämä jatkuu, kunnes tietokoneen muisti täyttyy ja saa aikaiseksi virheen stack overflow. Tässä tilanteessa Python generoi pitkän virheilmoituksen:
RuntimeError: maximum recursion depth exceeded

Virheilmoitus tulee, kun tietokoneen suorituspuskuri täyttyy.

19.3 Rekursion kontrollointi

Rekursion kontrolloimiseksi tarvitaan jokin keino, jolla voidaan välttää loputon funktion itsensä kutsu uudelleen ja uudelleen. Alla esimerkissä kutsukertojen määrää tarkastellaan if lauseessa ja kymmenen kerran täytyttyä, if lohkoa ei enää suoriteta ja rekursio päättyy.

def f(level):
    # Pring the level we are at
    print("Recursion call, level",level)
    # If we haven't reached level ten...
    if level < 10:
        # Call this function again
        # and add one to the level
        f(level+1)

# Start the recursive calls at level 1
f(1)

Recursion call, level 1
Recursion call, level 2
Recursion call, level 3
Recursion call, level 4
Recursion call, level 5
Recursion call, level 6
Recursion call, level 7
Recursion call, level 8
Recursion call, level 9
Recursion call, level 10

19.4 Kertoman rekursiivinen laskeminen

Kaikki rekursiivisesti ratkaistavat ohjelmointiprobleemat, jotka voidaan ratkaista rekursiivisesti, voidaan ratkaista myös ilman rekursiota. Jotkut ohjelmoijat pitävät rekursiivista tapaa ymmärrettävämpänä.

Kertoman laskeminen on klassinen esimerkki rekursiosta. Kertomaa käytetään esim. todennäköisyyslaskennassa. Esimerkiksi:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$

Rekursiivisesti tämä voidaan määritellä:
$n! = \begin{cases} 1 & \text{if } n = 0, \\ n \cdot (n-1)! & \text{if } n > 0. \end{cases}$

Alla on kaksi esimerkkiä, joissa lasketaan $n!$. Ensinnä on ei-rekursiivinen esimerkki ja toinen on sitten rekursiivinen koodi.

# This program calculates a factorial
# WITHOUT using recursion
def factorial_nonrecursive(n):
    answer = 1
    for i in range(2, n + 1):
        answer = answer * i
    return answer

# This program calculates a factorial
# WITH recursion
def factorial_recursive(n):
    if n == 1:
        return n
    else:
        return n * factorial_recursive(n - 1)

Alla esimerkissä on molemmat koodit yhdistetty samaan tiedostoon. Koodiin on lisätty muutamia print lauseita, jotta funktioiden tapahtumat on helpompi havainnoida.

# This program calculates a factorial
# WITHOUT using recursion

def factorial_nonrecursive(n):
    answer = 1
    for i in range(2, n + 1):
        print(i, "*", answer, "=", i * answer)
        answer = answer * i
    return answer

print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_nonrecursive(n)
print(answer)

# This program calculates a factorial
# WITH recursion

def factorial_recursive(n):
    if n == 1:
        return n
    else:
        x = factorial_recursive(n - 1)
        print( n, "*", x, "=", n * x )
        return n * x

print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_recursive(n)
print(answer)

I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040
I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040

19.5 Rekursiiviset suorakulmiot

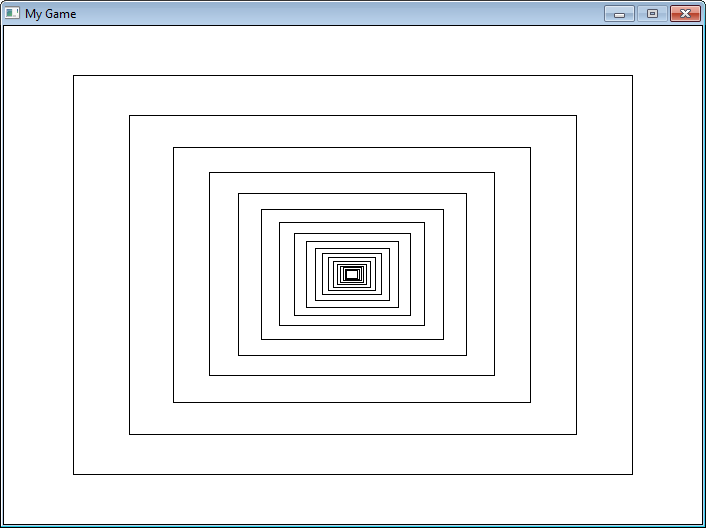
Rekursio voidaan esittää visuaalisesti seuraavalla Pygame ohjelmalla, 19.4, jossa rekursiivisesti piirretään sisäkkäisiä suorakulmioita. Seuraava suorakulmio on 20% pienempi kuin edellinen. Katso koodia tarkemmin ja rekursiivinen funktiokutsu recursive_draw.

"""
 Recursively draw rectangles.

 Sample Python/Pygame Programs
 Simpson College Computer Science
 http://programarcadegames.com/
 http://simpson.edu/computer-science/

"""
import pygame

# Colors
BLACK = (0, 0, 0)
WHITE = (255, 255, 255)


def recursive_draw(x, y, width, height):
    """ Recursive rectangle function. """
    pygame.draw.rect(screen, BLACK,
                     [x, y, width, height],
                     1)

    # Is the rectangle wide enough to draw again?
    if(width > 14):
        # Scale down
        x += width * .1
        y += height * .1
        width *= .8
        height *= .8
        # Recursively draw again
        recursive_draw(x, y, width, height)

pygame.init()

# Set the height and width of the screen
size = [700, 500]
screen = pygame.display.set_mode(size)

pygame.display.set_caption("My Game")

# Loop until the user clicks the close button.
done = False

# Used to manage how fast the screen updates
clock = pygame.time.Clock()

# -------- Main Program Loop -----------
while not done:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True

    # Set the screen background
    screen.fill(WHITE)

    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    recursive_draw(0, 0, 700, 500)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT

    # Go ahead and update the screen with what we've drawn.
    pygame.display.flip()

    # Limit to 60 frames per second
    clock.tick(60)

# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()

19.6 Fraktaalit

Fraktaalit on määritelty rekursiivisesti. Tässä esimerkissä on yksinkertainen fraktaali, joka muuttuu rekursion “syvyyden” mukaan.

"""
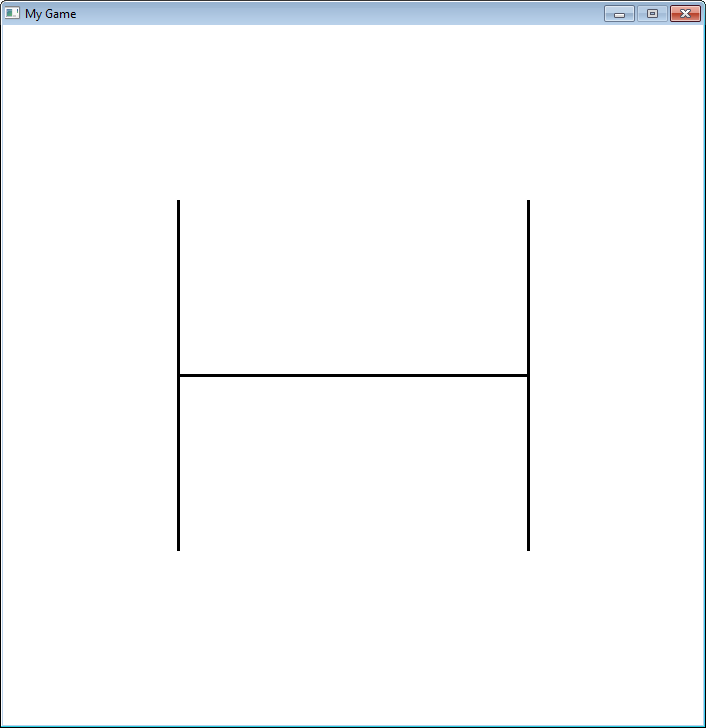
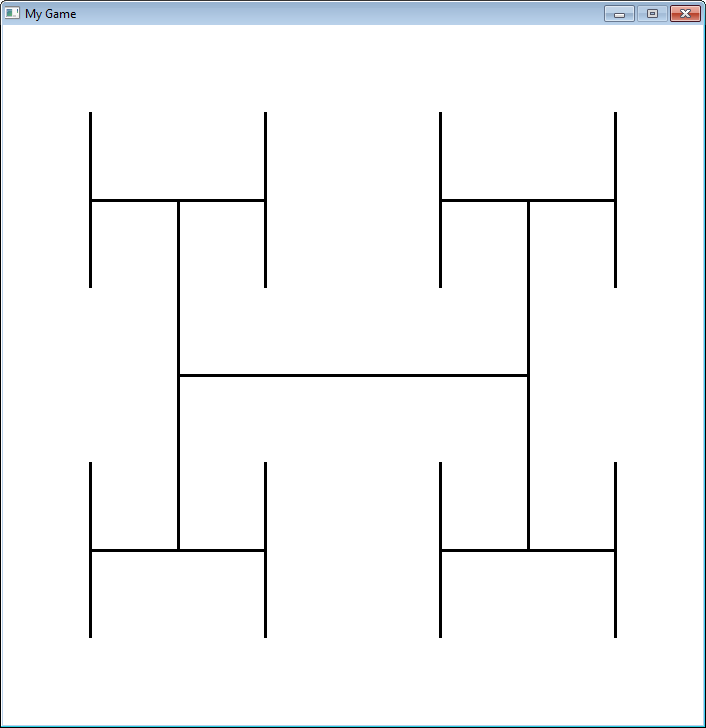
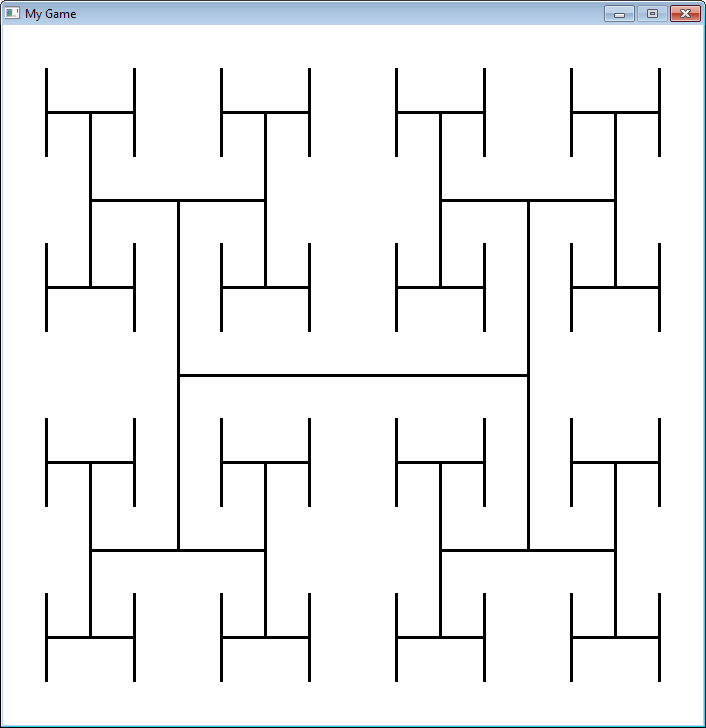
 Sample fractal using recursion.

 Sample Python/Pygame Programs
 Simpson College Computer Science
 http://programarcadegames.com/
 http://simpson.edu/computer-science/
"""

import pygame

# Define some colors
black = (0, 0, 0)
white = (255, 255, 255)
green = (0, 255, 0)
red = (255, 0, 0)


def recursive_draw(x, y, width, height, count):
    # Draw the rectangle
    # pygame.draw.rect(screen,black,[x,y,width,height],1)
    pygame.draw.line(screen,
                     black,
                     [x + width*.25, height // 2 + y],
                     [x + width*.75, height // 2 + y],
                     3)
    pygame.draw.line(screen,
                     black,
                     [x + width * .25, (height * .5) // 2 + y],
                     [x + width * .25,  (height * 1.5) // 2 + y],
                     3)
    pygame.draw.line(screen,
                     black,
                     [x + width * .75, (height * .5) // 2 + y],
                     [x + width * .75, (height * 1.5) // 2 + y],
                     3)

    if count > 0:
        count -= 1
        # Top left
        recursive_draw(x, y, width // 2, height // 2, count)
        # Top right
        recursive_draw(x + width // 2, y, width // 2, height // 2, count)
        # Bottom left
        recursive_draw(x, y + width // 2, width // 2, height // 2, count)
        # Bottom right
        recursive_draw(x + width // 2, y + width // 2, width // 2, height // 2, count)


pygame.init()

# Set the height and width of the screen
size = [700, 700]
screen = pygame.display.set_mode(size)

pygame.display.set_caption("My Game")

# Loop until the user clicks the close button.
done = False

# Used to manage how fast the screen updates
clock = pygame.time.Clock()

# -------- Main Program Loop -----------
while not done:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True

    # Set the screen background
    screen.fill(white)

    # ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
    fractal_level = 3
    recursive_draw(0, 0, 700, 700, fractal_level)
    # ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT

    # Go ahead and update the screen with what we've drawn.
    pygame.display.flip()

    # Limit to 20 frames per second
    clock.tick(20)

# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()

19.7 Rekursiivinen binaarihaku

Rekursiota voidaan käyttää binaarihaussa. Tässä on ensin esimerkki ei-rekursiivisesta ratkaisusta, joka esitettiin kappaleessa 15:

def binary_search_nonrecursive(search_list, key):
    lower_bound = 0
    upper_bound = len(search_list) - 1
    found = False
    while lower_bound < upper_bound and found == False:
        middle_pos = (lower_bound + upper_bound) // 2
        if search_list[middle_pos] < key:
            lower_bound = middle_pos + 1
        elif list[middle_pos] > key:
            upper_bound = middle_pos
        else:
            found = True

    if found:
        print( "The name is at position",middle_pos)
    else:
        print( "The name was not in the list." )

binary_search_nonrecursive(name_list,"Morgiana the Shrew")

Sama binaarihaku on alla kirjoitettuna rekursiivisella ratkaisulla:

def binary_search_recursive(search_list, key, lower_bound, upper_bound):
    middle_pos = (lower_bound + upper_bound) // 2
    if search_list[middle_pos] < key:
        binary_search_recursive(search_list,
                                key,
                                middle_pos + 1,
                                upper_bound)
    elif search_list[middle_pos] > key:
        binary_search_recursive(search_list,
                                key,
                                lower_bound,
                                middle_pos )
    else:
        print("Found at position", middle_pos)

lower_bound = 0
upper_bound = len(name_list) - 1
binary_search_recursive(name_list,
                        "Morgiana the Shrew",
                        lower_bound,
                        upper_bound)

19.8 Review

19.8.1 Short Answer Worksheet

Klikkaa tästä kappaleen kertaustehtäviin.