Programar Juegos Arcadecon Python y Pygame
Chapter 19: Recursividad
La pequeña niña no podía dormir, entonces, su mamá le contó la historia de una ranita,
que no podía dormir, entonces, la mamá de la ranita le contó la historia de un osito,
que no podía dormir, entonces, la mamá del osito le contó la historia de una pequeña comadreja...
que se durmió.
...y el pequeño osito se durmió;
...y la ranita se durmió;
...y la niña se durmió.
(Fuente: http://everything2.com/title/recursion)
La recursividad es un objeto o proceso que se define en términos de sí mismo. Ciertos patrones matemáticos como los factoriales y la sucesión de Fibonacci son recursivos. Documentos que contienen documentos que a su vez contienen otros documentos, son recursivos. Las imágenes fractales y ciertos procesos biológicos son recursivos en su forma de producirse.
19.1 ¿Dónde Utilizamos la Recursividad?
Ciertos documentos, como las páginas webs, son en esencia recursivos. Por ejemplo, la Figura 19.1 nos muestra
un documento web.
Ese documento puede estar dentro de una “caja,” la cual ayuda a estructurar el contenido de la página, tal como se ve en
la Figura 19.2.
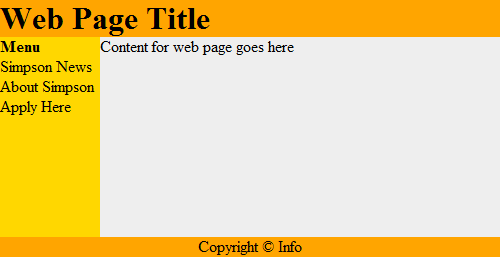
Esto funciona recursivamente. Cada caja contiene una página web, que puede tener una caja, la cual podría contener otra página
web, tal como vemos en la Figura 19.3.
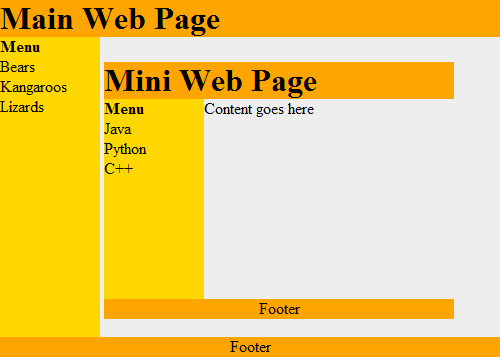
A menudo empleamos funciones recursivas para búsquedas avanzadas y algoritmos de ordenamiento. Veremos algunas de ellas aquí, y si en algún momento sigues un curso sobre “estructura de datos”, verás seguramente muchas más.
Aún en el caso de que una persona no se convierta en programadora, comprender el concepto de los sistemas recursivos es importante. Si en un determinado proyecto surgiera la necesidad de trabajar con tablas, documentos, o cosas por el estilo, recursivos, es importante saber cómo explicar esto a la persona que vaya a encargarse de la programación.
Supongamos, por ejemplo, que alguien quisiera que su web de recetas tuviese la capacidad de mantener una lista con ingredientes e instrucciones. Ahora, imaginemos una segunda persona familiarizada con la recursividad, la cual podría plantear que, en lugar de hacer listas, tengamos la capacidad de combinar ingredientes, con lo que obtendríamos recetas. Este segundo sistema es evidentemente más efectivo.
19.2 ¿De Qué Forma Codificamos la Recursividad?
En anteriores capítulos hemos usado funciones que llamaban a otras funciones. Por ejemplo:
def f():
g()
print("f")
def g():
print("g")
f()
También es posible que una función se llame a sí misma. Es decir, haciendo uso de un concepto llamado recursividad. Por ejemplo:
def f():
print("Hola")
f()
f()
El ejemplo anterior imprimirá Hola y luego llamará otra vez a la función f(). Esto provocará que se imprima otro
Hola y que vuelva a llamarse a f(). Esto seguirá haciéndose hasta que el ordenador se quede sin algo llamado
stack space (espacio de pila). Cuando sucede esto, Python mostrará un largo error que finaliza con:
RuntimeError: maximum recursion depth exceeded
El ordenador te está diciendo, a ti programador, que has ido demasiado lejos en la madriguera.
19.3 Controlar la Profundidad de la Recursividad
Para usar eficientemente la recursividad, tiene que existir una forma que evite que la función se llame a sí misma una y otra vez. El siguiente ejemplo cuenta las veces se ha llamado, y usa una declaración if para salir cuando la función se llama a sí misma diez veces.
def f(nivel):
# Imprime el nivel en el que nos encontramos
print("Llamada de recursividad, nivel",nivel)
# Si aún no hemos llegado al nivel ten...
if nivel < 10:
# Llama otra vez a la función
# y suma uno al nivel
f(nivel+1)
# Comienza las llamadas recursivas en el nivel 1
f(1)
|
Output:
Llamada de recursividad, nivel 1 Llamada de recursividad, nivel 2 Llamada de recursividad, nivel 3 Llamada de recursividad, nivel 4 Llamada de recursividad, nivel 5 Llamada de recursividad, nivel 6 Llamada de recursividad, nivel 7 Llamada de recursividad, nivel 8 Llamada de recursividad, nivel 9 Llamada de recursividad, nivel 10 |
19.4 Cálculo Factorial Usando Recursividad
Cualquier código que pueda hacerse con recursividad, también lo puede hacer sin ella. Algunos programadores piensan que el código recursivo es más fácil de entender.
Calcular el factorial de un número es un ejemplo clásico del uso de la recursividad. Los factoriales son muy útiles en
probabilidad y estadística. Por ejemplo:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$
Recursivamente puede describirse así:
$n! = \begin{cases} 1 & \text{if } n = 0, \\ n \cdot (n-1)! & \text{if } n > 0. \end{cases}$
Aquí debajo hay dos ejemplos de funciones que calculan $n!$. La primera no emplea la recursividad, la segunda sí.
# Este programa calcula el factorial de un número
# SIN emplear recursividad
def factorial_norecursivo(n):
respuesta = 1
for i in range(2, n+1):
respuesta = respuesta * i
return respuesta
# Este programa calcula el factorial de un número
# USANDO recursividad
def factorial_recursivo(n):
if(n == 1):
return n
else:
return n * factorial_recursivo(n-1)
Por sí solas estas funciones no hacen nada. Debajo hay un ejemplo donde unimos todo. En él hemos añadido algunas sentencias print a la función, lo que nos permitirá ver que está sucediendo.
# Este programa calcula el factorial de un número
# SIN emplear recursividad
def factorial_norecursivo(n):
respuesta = 1
for i in range(2, n+1):
print(i,"*",respuesta,"=", i*respuesta)
respuesta = respuesta * i
return respuesta
print("Puedo calcular un factorial!")
entrada_usuario = input ("Introduce un número: ")
n = int(entrada_usuario)
respuesta = factorial_norecursivo(n)
print(respuesta)
# Este programa calcula el factorial de un número
# USANDO recursividad
def factorial_recursivo(n):
if( n == 1 ):
return n
else:
x = factorial_recursivo(n-1)
print( n, "*", x, "=", n * x )
return n * x
print("Puedo calcular un factorial!")
entrada_usuario = input ("Introduce un número:")
n = int(entrada_usuario)
respuesta = factorial_recursivo(n)
print(respuesta)
|
Output:
Puedo calcular un factorial! Introduce un número:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 Puedo calcular un factorial! Introduce un número:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 |
19.5 Rectángulos Recursivos
La recursividad es fantástica para trabajar con documentos estructurados que a su vez son recursivos. Por ejemplo, un documento web que tiene una tabla dividida en filas y columnas para ayudar en el diseño. Una fila podría ser el encabezado, otra el cuerpo principal, y finalmente, otra para el pie. Dentro de una de las celdas podría ir otra tabla. Y, dentro de ésta, una tabla más.
Otro ejemplo son los e-mail. Es posible adjuntar el e-mail de otra persona al tuyo. Pero este e-mail podría tener otro e-mail adjunto, y así sucesivamente.
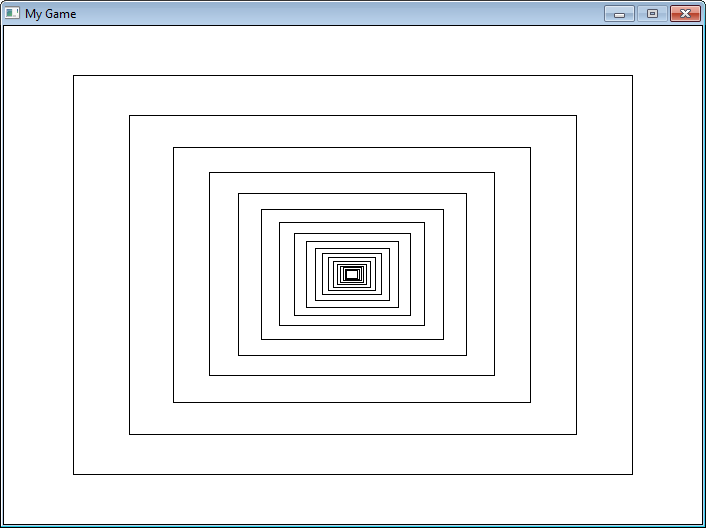
¿Podemos observar en acción la recursividad en alguno de nuestros programas Pygame? Sí! La Figura 19.4muestra un ejemplo que dibuja un rectángulo, y recursivamente, continúa dibujando rectángulos dentro de éste. Cada nuevo
rectángulo es un 20% más pequeño que el anterior. Observa el código. Presta especial atención a llamada de recursividad en
la función recursive_draw.
"""
Dibujaremos rectángulos de forma recursiva.
Sample Python/Pygame Programs
Simpson College Computer Science
http://programarcadegames.com/
http://simpson.edu/computer-science/
"""
import pygame
# Definimos algunos colores
NEGRO = (0, 0, 0)
BLANCO = (255, 255, 255)
def dibujo_recursivo(x, y, largo, alto):
""" Función para dibujar recursivamente rectángulos. """
pygame.draw.rect(pantalla, NEGRO,
[x,y,largo,alto],
1)
# Es el rectángulo lo bastante largo como para volver a dibujarlo?
if(largo > 14):
# Reducimos
x += largo * .1
y += alto * .1
largo *= .8
alto *= .8
# Lo dibujamos otra vez recursivamente
dibujo_recursivo(x, y, largo, alto)
pygame.init()
# Establecemos el alto y largo de la pantalla
dimensiones = [700, 500]
pantalla = pygame.display.set_mode(dimensiones)
pygame.display.set_caption("Mi Juego")
# Iteramos hasta que el usuario haga click sobre el botón de cerrar
hecho = False
# Usado para gestionar cuán rápido se actualiza la pantalla
reloj = pygame.time.Clock()
# -------- Bucle Principal del Programa -----------
while not hecho:
for evento in pygame.event.get():
if evento.type == pygame.QUIT:
hecho = True
# Limpia la pantalla y establece su color de fondo
pantalla.fill(BLANCO)
# TODO EL CÓDIGO DE DIBUJO DEBERÍA IR DEBAJO DE ESTE COMENTARIO
dibujo_recursivo(0, 0, 700, 500)
# TODO EL CÓDIGO DE DIBUJO DEBERÍA IR ENCIMA DE ESTE COMENTARIO
# # Avancemos y actualicemos la pantalla con lo que hemos dibujado.
pygame.display.flip()
# Limitamos a 60 fotogramas por segundo
reloj.tick(60)
# Pórtate bien con el IDLE. Si nos olvidamos de esta línea, el programa se 'colgará'
# en la salida.
pygame.quit()
19.6 Fractales
Los fractales son definidos recursivamente. Aquí puedes observar un fractal muy básico, que nos muestra cómo cambia, en
función de cuan “profunda” sea la recursividad.
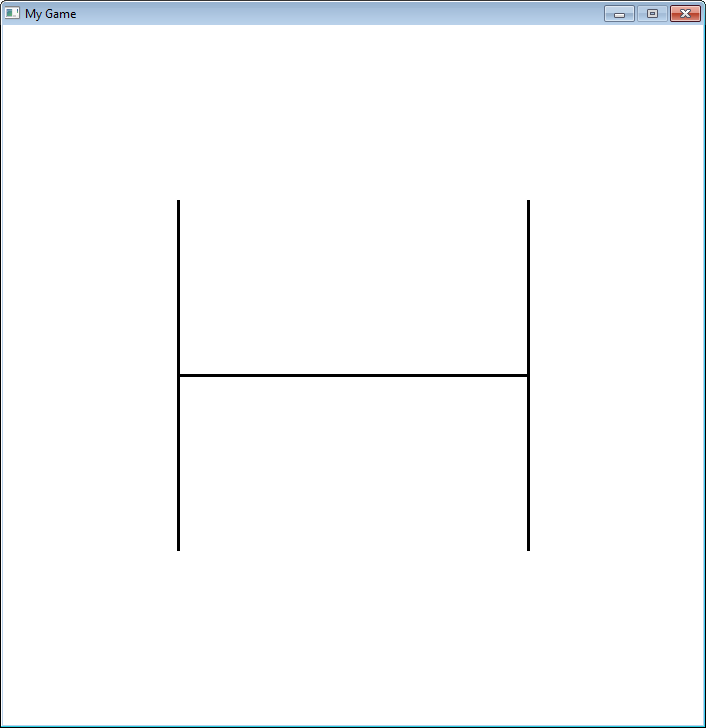
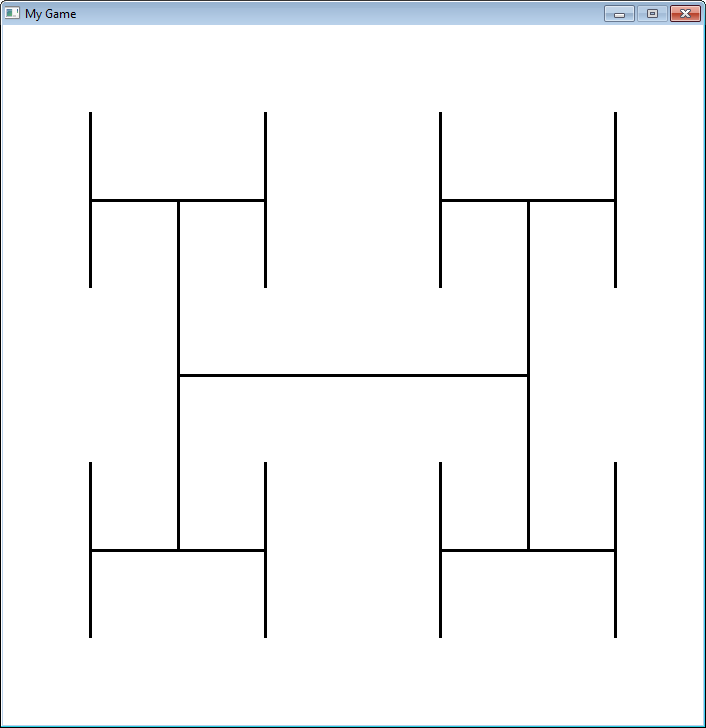
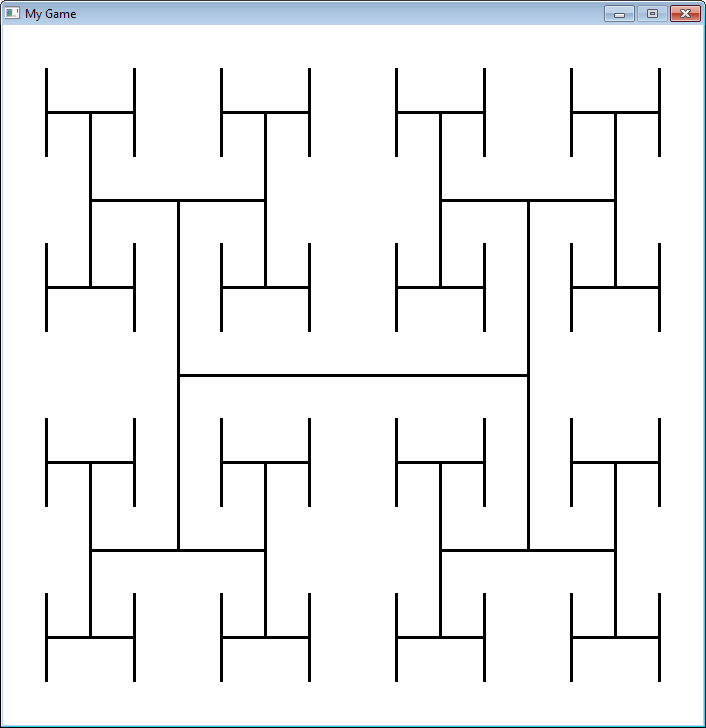

"""
Ejemplo de Fractales usando recursividad
Sample Python/Pygame Programs
Simpson College Computer Science
http://programarcadegames.com/
http://simpson.edu/computer-science/
"""
import pygame
# Definimos algunos colores
NEGRO = (0, 0, 0)
BLANCO = (255, 255, 255)
def dibujo_recursivo(x, y, largo, alto, cuenta):
# Dibujamos el rectángulo
# pygame.draw.rect(pantalla,NEGRO,[x,y,largo,alto],1)
pygame.draw.line(pantalla,
NEGRO,
[x + largo*.25,alto//2+y],
[x + largo*.75,alto//2+y],
3)
pygame.draw.line(pantalla,
NEGRO,
[x+largo*.25,(alto*.5)//2+y],
[x+largo*.25,(alto*1.5)//2+y],
3)
pygame.draw.line(pantalla,
NEGRO,
[x + largo*.75,(alto*.5)//2+y],
[x + largo*.75,(alto*1.5)//2+y],
3)
if cuenta > 0:
cuenta -= 1
# Arriba izquierda
dibujo_recursivo(x, y, largo // 2, alto // 2, cuenta)
# Arriba derecha
dibujo_recursivo(x + largo // 2, y, largo // 2, alto // 2, cuenta)
# Abajo izquierda
dibujo_recursivo(x, y + largo // 2, largo // 2, alto // 2, cuenta)
# Abajo derecha
dibujo_recursivo(x + largo // 2, y + largo // 2, largo // 2, alto // 2, cuenta)
pygame.init()
# Establecemos el alto y largo de la pantalla
dimensiones = [700, 500]
pantalla = pygame.display.set_mode(dimensiones)
pygame.display.set_caption("Mi Juego")
#Iteramos hasta que el usuario haga click sobre el botón de cerrar
hecho = False
# Usado para gestionar cuán rápido se actualiza la pantalla
reloj = pygame.time.Clock()
# -------- Bucle Principal del Programa -----------
while not hecho:
for evento in pygame.event.get(): # El usuario hizo algo
if evento.type == pygame.QUIT: # Si el usuario hace click sobre cerrar
hecho = True # Marca que ya lo hemos hecho, de forma que abandonamos el bucle
# Limpia la pantalla y establece su color de fondo
pantalla.fill(BLANCO)
# TODO EL CÓDIGO DE DIBUJO DEBERÍA IR DEBAJO DE ESTE COMENTARIO
nivel_fractal = 3
dibujo_recursivo(0, 0, 700, 700, nivel_fractal)
# TODO EL CÓDIGO DE DIBUJO DEBERÍA IR ENCIMA DE ESTE COMENTARIO
# # Avancemos y actualicemos la pantalla con lo que hemos dibujado.
pygame.display.flip()
# Limitamos a 20 fotogramas por segundo
reloj.tick(20)
# Pórtate bien con el IDLE. Si nos olvidamos de esta línea, el programa se 'colgará'
# en la salida.
pygame.quit()
19.7 Búsqueda Binaria Recursiva
También podemos usar la recursividad para hacer búsquedas binarias. Aquí debajo hay una búsqueda binaria no recursiva del Capítulo 17:
def busqueda_binaria_norecursiva(lista_busqueda, clave):
limite_inferior = 0
limite_superior = len(lista_busqueda) - 1
encontrado = False
while limite_inferior < limite_superior and encontrado == False:
pos_intermedia = (limite_inferior + limite_superior) // 2
if lista_busqueda[pos_intermedia] < clave:
limite_inferior = pos_intermedia + 1
elif list[pos_intermedia] > clave:
limite_superior = pos_intermedia
else:
encontrado = True
if encontrado:
print("El nombre se encuentra en la posición",pos_intermedia)
else:
print("El nombre no estaba en la lista.")
busqueda_binaria_norecursiva(nombre_en_lista,"Morgiana la Arpía")
La misma búsqueda binaria pero ahora usando recursividad:
def busqueda_binaria_recursiva(lista_busqueda,clave, limite_inferior, limite_superior):
pos_intermedia = (limite_inferior + limite_superior) // 2
if lista_busqueda[pos_intermedia] < clave:
busqueda_binaria_recursiva(lista_busqueda,
clave,
pos_intermedia + 1,
limite_superior)
elif lista_busqueda[pos_intermedia] > clave:
busqueda_binaria_recursiva(lista_busqueda,
clave,
limite_inferior,
pos_intermedia )
else:
print("Encontrado en la posición", pos_intermedia)
limite_inferior = 0
limite_superior = len(nombre_en_lista) - 1
busqueda_binaria_recursiva(nombre_en_lista,
"Morgiana la Arpía",
limite_inferior,
limite_superior)
19.8 Repaso
19.8.1 Test
Haz click para ir a los Ejercicios.
English version by Paul Vincent Craven
Spanish version by Antonio Rodríguez Verdugo
Russian version by Vladimir Slav
Turkish version by Güray Yildirim
Portuguese version by Armando Marques Sobrinho and Tati Carvalho
Dutch version by Frank Waegeman
Hungarian version by Nagy Attila
Finnish version by Jouko Järvenpää
French version by Franco Rossi
Korean version by Kim Zeung-Il
Chinese version by Kai Lin