Program Arcade GamesWith Python And Pygame
Chapter 19: Recursion
A child couldn't sleep, so her mother told her a story about a little frog,
who couldn't sleep, so the frog's mother told her a story about a little bear,
who couldn't sleep, so the bear's mother told her a story about a little weasel...
who fell asleep.
...and the little bear fell asleep;
...and the little frog fell asleep;
...and the child fell asleep.
(Source: http://everything2.com/title/recursion)
Recursion is an object or process that is defined in terms of itself. Mathematical patterns such as factorials and the Fibonacci series are recursive. Documents that can contain other documents, which themselves can contain other documents, are recursive. Fractal images, and even certain biological processes are recursive in how they work.
19.1 Where is Recursion Used?
Documents, such as web pages, are naturally recursive. For example,
Figure 19.1 shows a web document.
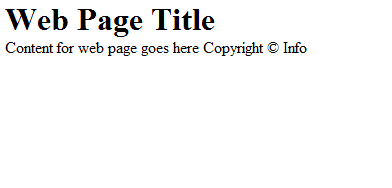
That web document can be contained in a “box,” which can help layout the page
as shown in Figure 19.2.
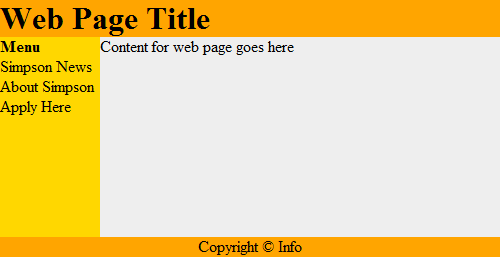
This works recursively. Each box can contain a web page, that can have a
box, which could contain another web page as shown in Figure 19.3.
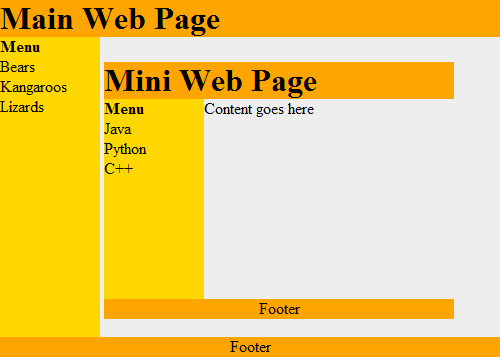
Recursive functions are often used with advanced searching and sorting algorithms. We'll show some of that here and if you take a “data structures” class you will see a lot more of it.
Even if a person does not become a programmer, understanding the concept of recursive systems is important. If there is a business need for recursive table structures, documents, or something else, it is important to know how to specify this to the programmer up front.
For example, a person might specify that a web program for recipes needs the ability to support ingredients and directions. A person familiar with recursion might state that each ingredient could itself be a recipes with other ingredients (that could be recipes.) The second system is considerably more powerful.
19.2 How is Recursion Coded?
In prior chapters, we have used functions that call other functions. For example:
def f():
g()
print("f")
def g():
print("g")
f()
It is also possible for a function to call itself. A function that calls itself is using a concept called recursion. For example:
def f():
print("Hello")
f()
f()
The example above will print Hello and then call
the f() function
again. Which will cause another Hello to be printed out and
another call to the f() function. This will continue until the computer runs out
of something called stack space. When this happens, Python will output a
long error that ends with:
RuntimeError: maximum recursion depth exceeded
The computer is telling you, the programmer, that you have gone too far down the rabbit hole.
19.3 Controlling Recursion Depth
To successfully use recursion, there needs to be a way to prevent the function from endlessly calling itself over and over again. The example below counts how many times it has been called, and uses an if statement to exit once the function has called itself ten times.
def f(level):
# Print the level we are at
print("Recursion call, level",level)
# If we haven't reached level ten...
if level < 10:
# Call this function again
# and add one to the level
f(level+1)
# Start the recursive calls at level 1
f(1)
|
Output:
Recursion call, level 1 Recursion call, level 2 Recursion call, level 3 Recursion call, level 4 Recursion call, level 5 Recursion call, level 6 Recursion call, level 7 Recursion call, level 8 Recursion call, level 9 Recursion call, level 10 |
19.4 Recursion Factorial Calculation
Any code that can be done recursively can be done without using recursion. Some programmers feel that the recursive code is easier to understand.
Calculating the factorial of a number is a classic example of
using recursion. Factorials are useful in probability and statistics.
For example:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$
Recursively, this can be described as:
$n! = \begin{cases} 1 & \text{if } n = 1, \\ n \cdot (n-1)! & \text{if } n > 1. \end{cases}$
Below are two example functions that calculate $n!$. The first one is non-recursive, the second is recursive.
# This program calculates a factorial
# WITHOUT using recursion
def factorial_nonrecursive(n):
answer = 1
for i in range(2, n + 1):
answer = answer * i
return answer
# This program calculates a factorial
# WITH recursion
def factorial_recursive(n):
if n == 1:
return 1
elif n > 1:
return n * factorial_recursive(n - 1)
The functions do nothing by themselves. Below is an example where we put it all together. This example also adds some print statements inside the function so we can see what is happening.
# This program calculates a factorial
# WITHOUT using recursion
def factorial_nonrecursive(n):
answer = 1
for i in range(2, n + 1):
print(i, "*", answer, "=", i * answer)
answer = answer * i
return answer
print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_nonrecursive(n)
print(answer)
# This program calculates a factorial
# WITH recursion
def factorial_recursive(n):
if n == 1:
return 1
else:
x = factorial_recursive(n - 1)
print( n, "*", x, "=", n * x )
return n * x
print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_recursive(n)
print(answer)
|
Output:
I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 I can calculate a factorial! Enter a number:7 2 * 1 = 2 3 * 2 = 6 4 * 6 = 24 5 * 24 = 120 6 * 120 = 720 7 * 720 = 5040 5040 |
19.5 Recursive Rectangles
Recursion is great to work with structured documents that are themselves recursive. For example, a web document can have a table divided into rows and columns to help with layout. One row might be the header, another row the main body, and finally the footer. Inside a table cell, might be another table. And inside of that can exist yet another table.
Another example is e-mail. It is possible to attach another person's e-mail to a your own e-mail. But that e-mail could have another e-mail attached to it, and so on.
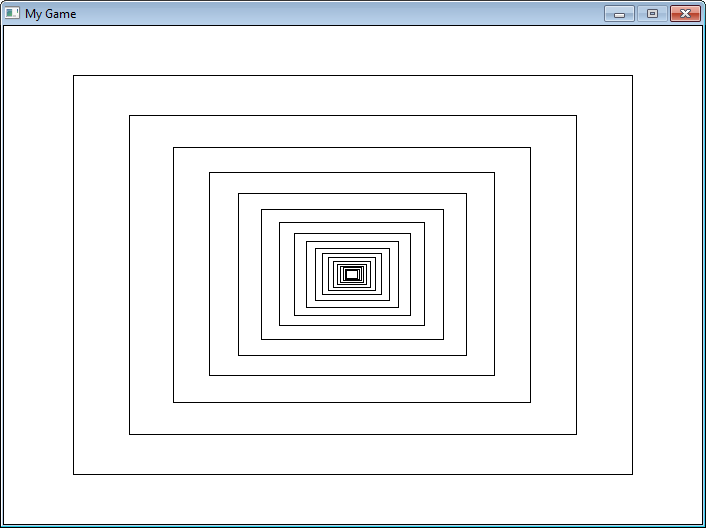
Can we visually see recursion in action in one of our Pygame programs?
Yes! Figure 19.4 shows
an example program that draws a rectangle, and recursively keeps drawing
rectangles inside of it. Each rectangle is 20% smaller than the parent rectangle.
Look at the code. Pay close attention to the
recursive call in the recursive_draw function.
"""
Recursively draw rectangles.
Sample Python/Pygame Programs
Simpson College Computer Science
http://programarcadegames.com/
http://simpson.edu/computer-science/
"""
import pygame
# Colors
BLACK = (0, 0, 0)
WHITE = (255, 255, 255)
def recursive_draw(x, y, width, height):
""" Recursive rectangle function. """
pygame.draw.rect(screen, BLACK,
[x, y, width, height],
1)
# Is the rectangle wide enough to draw again?
if(width > 14):
# Scale down
x += width * .1
y += height * .1
width *= .8
height *= .8
# Recursively draw again
recursive_draw(x, y, width, height)
pygame.init()
# Set the height and width of the screen
size = [700, 500]
screen = pygame.display.set_mode(size)
pygame.display.set_caption("My Game")
# Loop until the user clicks the close button.
done = False
# Used to manage how fast the screen updates
clock = pygame.time.Clock()
# -------- Main Program Loop -----------
while not done:
for event in pygame.event.get():
if event.type == pygame.QUIT:
done = True
# Set the screen background
screen.fill(WHITE)
# ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
recursive_draw(0, 0, 700, 500)
# ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT
# Go ahead and update the screen with what we've drawn.
pygame.display.flip()
# Limit to 60 frames per second
clock.tick(60)
# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()
19.6 Fractals
Fractals are defined recursively. Here is a very simple fractal, showing how it changes
depending on how “deep” the recursion goes.
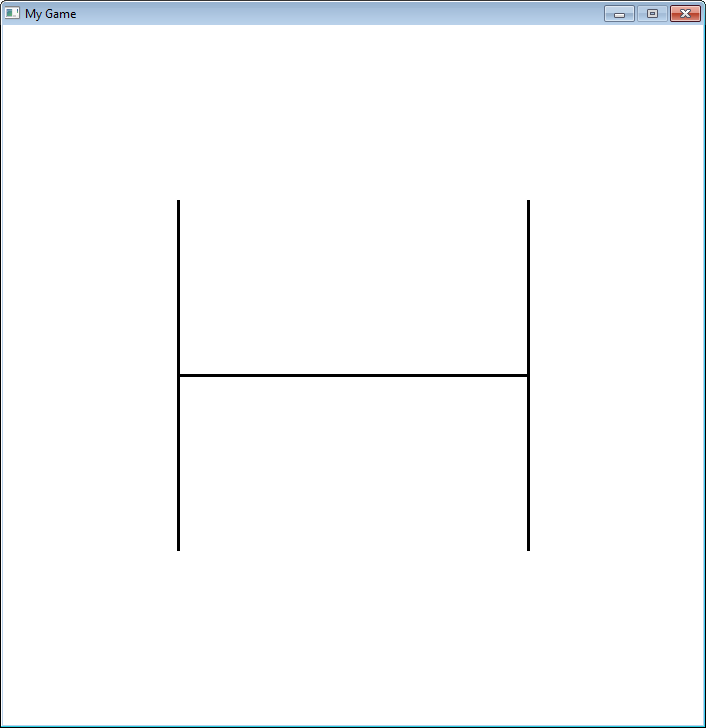
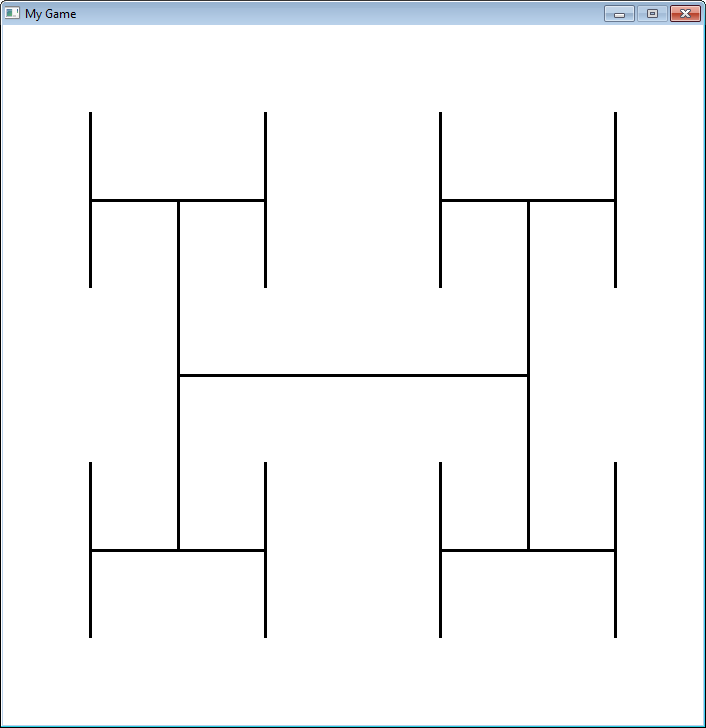
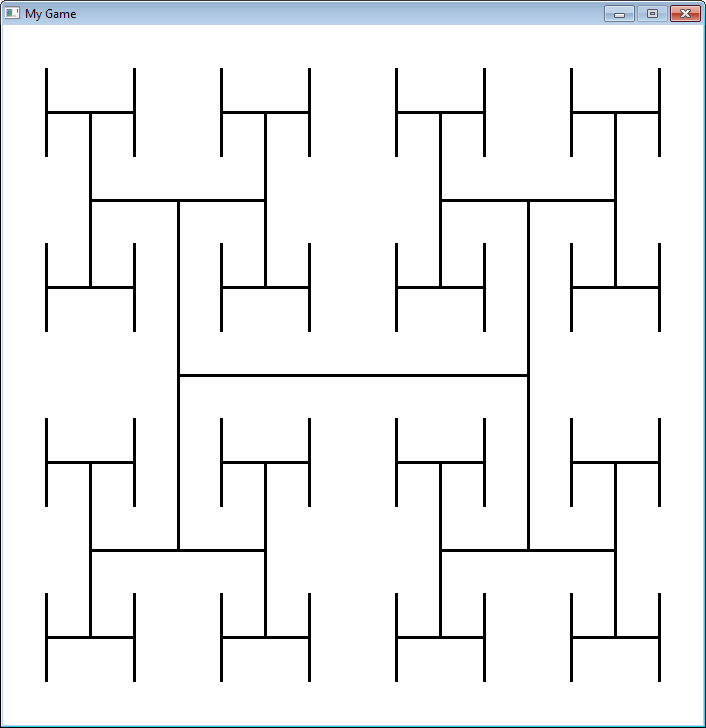

"""
Sample fractal using recursion.
Sample Python/Pygame Programs
Simpson College Computer Science
http://programarcadegames.com/
http://simpson.edu/computer-science/
"""
import pygame
# Define some colors
black = (0, 0, 0)
white = (255, 255, 255)
green = (0, 255, 0)
red = (255, 0, 0)
def recursive_draw(x, y, width, height, count):
# Draw the rectangle
# pygame.draw.rect(screen,black,[x,y,width,height],1)
pygame.draw.line(screen,
black,
[x + width*.25, height // 2 + y],
[x + width*.75, height // 2 + y],
3)
pygame.draw.line(screen,
black,
[x + width * .25, (height * .5) // 2 + y],
[x + width * .25, (height * 1.5) // 2 + y],
3)
pygame.draw.line(screen,
black,
[x + width * .75, (height * .5) // 2 + y],
[x + width * .75, (height * 1.5) // 2 + y],
3)
if count > 0:
count -= 1
# Top left
recursive_draw(x, y, width // 2, height // 2, count)
# Top right
recursive_draw(x + width // 2, y, width // 2, height // 2, count)
# Bottom left
recursive_draw(x, y + width // 2, width // 2, height // 2, count)
# Bottom right
recursive_draw(x + width // 2, y + width // 2, width // 2, height // 2, count)
pygame.init()
# Set the height and width of the screen
size = [700, 700]
screen = pygame.display.set_mode(size)
pygame.display.set_caption("My Game")
# Loop until the user clicks the close button.
done = False
# Used to manage how fast the screen updates
clock = pygame.time.Clock()
# -------- Main Program Loop -----------
while not done:
for event in pygame.event.get():
if event.type == pygame.QUIT:
done = True
# Set the screen background
screen.fill(white)
# ALL CODE TO DRAW SHOULD GO BELOW THIS COMMENT
fractal_level = 3
recursive_draw(0, 0, 700, 700, fractal_level)
# ALL CODE TO DRAW SHOULD GO ABOVE THIS COMMENT
# Go ahead and update the screen with what we've drawn.
pygame.display.flip()
# Limit to 20 frames per second
clock.tick(20)
# Be IDLE friendly. If you forget this line, the program will 'hang'
# on exit.
pygame.quit()
19.7 Recursive Binary Search
Recursion can be also be used to perform a binary search. Here is a non-recursive binary search from Chapter 15:
def binary_search_nonrecursive(search_list, key):
lower_bound = 0
upper_bound = len(search_list) - 1
found = False
while lower_bound < upper_bound and found == False:
middle_pos = (lower_bound + upper_bound) // 2
if search_list[middle_pos] < key:
lower_bound = middle_pos + 1
elif search_list[middle_pos] > key:
upper_bound = middle_pos
else:
found = True
if found:
print( "The name is at position",middle_pos)
else:
print( "The name was not in the list." )
binary_search_nonrecursive(name_list,"Morgiana the Shrew")
This same binary search written in a recursive manner:
def binary_search_recursive(search_list, key, lower_bound, upper_bound):
middle_pos = (lower_bound + upper_bound) // 2
if search_list[middle_pos] < key:
binary_search_recursive(search_list,
key,
middle_pos + 1,
upper_bound)
elif search_list[middle_pos] > key:
binary_search_recursive(search_list,
key,
lower_bound,
middle_pos )
else:
print("Found at position", middle_pos)
lower_bound = 0
upper_bound = len(name_list) - 1
binary_search_recursive(name_list,
"Morgiana the Shrew",
lower_bound,
upper_bound)
19.8 Review
19.8.1 Short Answer Worksheet
Click here for the chapter worksheet.
English version by Paul Vincent Craven
Spanish version by Antonio Rodríguez Verdugo
Russian version by Vladimir Slav
Turkish version by Güray Yildirim
Portuguese version by Armando Marques Sobrinho and Tati Carvalho
Dutch version by Frank Waegeman
Hungarian version by Nagy Attila
Finnish version by Jouko Järvenpää
French version by Franco Rossi
Korean version by Kim Zeung-Il
Chinese version by Kai Lin